
����Ŀ���ݡ��й���������2004��5��24�ձ�����Ŀǰȫ���н�3������Сѧ������У�����ñ�Ϊ���˽����3������СѧУ���Ľ�����������г�ȡ��4600��ѧУ������ЩѧУУ���Ľ�����������ʾ����飬�����ݴ����������ͼ������ͳ��ͼ��
˵����ͳ��ͼ1�İٷ�����![]() ��100%��
��100%��
ͳ��ͼ2�İٷ�����![]() ��100%��
��100%��
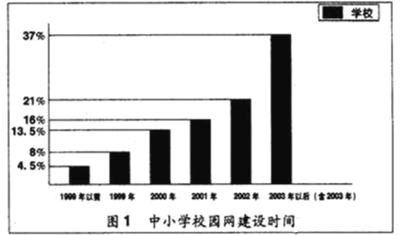
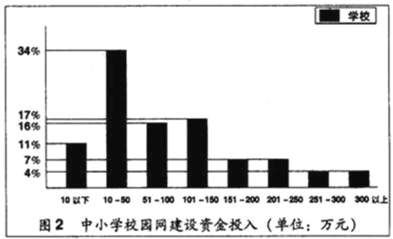
������������ֺ�ͳ��ͼ�ṩ����Ϣ�ش��������⣺
��1������������У�����ָʲô������������ʲô��
��2�����ƣ���ȫ���ѽ���У������Сѧ�У�
��У������ʱ����2003���Ժ�2003�꣩��ѧУ��Լ�ж�������
��У�������ʽ�Ͷ����200��Ԫ���ϣ�����200��Ԫ����ѧУ��Լ�ж�������
��3������ȡ��4600��ѧУ�У�У�������ʽ�Ͷ�����λ�������Ǹ��ʽ���ڣ�
��4��ͼ�л��ṩ��������Ϣ�����磺У�������ʽ�Ͷ����10��50��Ԫ����Сѧ���������ȣ�����д������������Ϣ��
���𰸡���1������ָȫ������У���Ľ�3������СѧУ�����������ȫ�壬���������ǽ�3������СѧУ�����г�ȡ��λ��Ŀ����2����11100����������4500����������3��У�������ʽ�Ͷ�����λ������51��Ԫ��100��Ԫ���ʽ���ڣ���4����ȫ��У�������ʽ�Ͷ����250��Ԫ���ϵ�ѧУ��Լ��2400������2003���Ժ�2003�꣩����У����ѧУ��ࣻ�۽�����Ϣ���ƽ�������Խ��Խ��
��������
��1���������⣬����ָȫ������У���Ľ�3������СѧУ�����������ȫ�壬���������ǽ�3������СѧУ�����г�ȡ��λ��Ŀ��
��2������Сѧ������У����������������ʱ����2003���Ժ�2003�꣩��ѧУ��ռ�ٷֱȣ�
����Сѧ������У�����������������ʽ�Ͷ����200��Ԫ���ϣ�����200��Ԫ����ѧУ��ռ�ٷֱȣ�
��3��У�������ʽ�Ͷ�����λ������51��Ԫ��100��Ԫ���ʽ���ڣ�
��4���𰸲�Ψһ���������ɣ�
�⣺��1������ָȫ������У���Ľ�3������СѧУ�����������ȫ�壬���������ǽ�3������СѧУ�����г�ȡ��λ��Ŀ��
��2����ȫ��У������ʵ����2003���Ժ�2003�꣩����Сѧ��Լ��37%��30000��11100��������
��ȫ��У�������ʽ�Ͷ����200��Ԫ���ϣ�����200��Ԫ������Сѧ��Լ�У�7%+4%+4%����30000��4500��������
��3��У�������ʽ�Ͷ�����λ������51��Ԫ��100��Ԫ���ʽ���ڣ�
��4����ȫ��У�������ʽ�Ͷ����250��Ԫ���ϵ�ѧУ��Լ��2400����
��2003���Ժ�2003�꣩����У����ѧУ��ࣻ
�۽�����Ϣ���ƽ�������Խ��Խ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Сǿ��A�������ر�ƫ��70���������ߣ�����B���������ű�ƫ��30������������C������ʱ��ѷ�������������ʱһ�£�����ĵ���Ӧ�ǣ�������
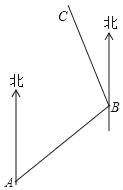
A. ��ת 80�� B. ��ת80�� C. ��ת 100�� D. ��ת 100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
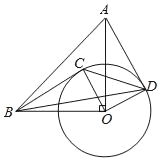
����Ŀ����ͼ����Rt��OAB�У���AOB��90����OA��OB��4���Ե�OΪԲ�ġ�2Ϊ�뾶��Բ����C�ǡ�O������һ�㣬����BC��OC����OC�Ƶ�O��˳ʱ�뷽����ת90��������O�ڵ�D������AD��
��1����AD���O����ʱ��
����֤��BC�ǡ�O�����ߣ�
�����C��OB�ľ��룮
��2������BD��CD������BCD��������ʱ����B��CD�ľ���Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���һ����ʽ�ܻ���һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽ����������ʽΪ����г��ʽ�����磺![]() ����
����![]() ������г��ʽ����
������г��ʽ����
(1)���з�ʽ�У���������г��ʽ������_____(�����)��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��
(2)������г��ʽ��![]() ����һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽΪ��
����һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽΪ��![]() ��_______(Ҫд�����ι���)��
��_______(Ҫд�����ι���)��
(3)Ӧ�ã��Ȼ���![]() ������xȡʲô����ʱ����ʽ��ֵΪ������
������xȡʲô����ʱ����ʽ��ֵΪ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
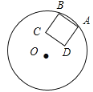
����Ŀ����ͼ��ƽ����һ����O�뾶Ϊ4��Բ������������A��B����ABΪ����Բ����һ��������ABDC����OD����Сֵ�ǣ�������
A.2B.![]() C.2
C.2![]() ��2D.4
��2D.4![]() ��4
��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx��a��0������E��8��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ࣩ����C��D���������ϣ���BAD��ƽ����AM��BC�ڵ�M����N��CD���е㣬��֪OA��2����OA��AD��1��3.
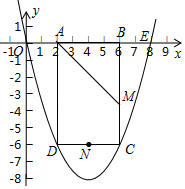
��1���������ߵĽ���ʽ��
��2��F��G�ֱ�Ϊx�ᣬy���ϵĶ��㣬˳������M��N��G��F�����ı���MNGF�����ı���MNGF�ܳ�����Сֵ��
��3����x���·��������������Ƿ���ڵ�P��ʹ��ODP��OD���ϵĸ�Ϊ![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��4������ABCD������������������ƽ�ƣ���ƽ�ƺ������������εı�����������K��L����ֱ��KLƽ�־��ε����ʱ����������ƽ�Ƶľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ij����һ��ָ�Ӵ���C���յ��洬��B������������źţ���ȷ����������ê���洬���ڵ�B��λ��C������ƫ��45�������ϣ���BC=60���ָ�Ӵ��������֣���C������ƫ��60����������һ�Һ��ബA��ǡ��λ��B������������.��������ബAǰ���Ѿȣ���֪���ബA�ĺ����ٶ�Ϊ30����/Сʱ�����洬��B����Ҫ�ȴ��ʱ����ܵõ����ബA�ľ�Ԯ�����ο����ݣ�![]() ��
��![]() ��
��![]() �����ȷ��0.1Сʱ��
�����ȷ��0.1Сʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̶ӳе���һ�γ�Ϊ1500�ĵ�·�̻����̣�ʩ��ʱ�������̻��������������̻�1�ĵ�·��ҪA�ͻ�2֦��B�ͻ�3֦���ɱ���22Ԫ���ҷ������̻�1�ĵ�·��ҪA�ͻ�1֦��B�ͻ�5֦���ɱ���25Ԫ.��Ҫ�����ҷ����̻���·���ܳ��Ȳ������ڰ������̻���·���ܳ��ȵ�2��.
(1)��A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ��Ƕ���Ԫ?
(2)�������̻��ĵ�·�ܳ���Ϊ������ʱ�����蹤�̵��ܳɱ�����?�ܳɱ������Ƕ���Ԫ?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com