
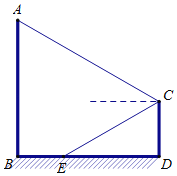
【题目】如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.
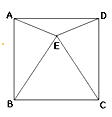
【答案】150°.
【解析】
由四边形ABCD是正方形和△BEC是正三角形,得出△BAE是等腰三角形,∠ABE=30°,由等腰三角形的性质得出∠BAE=75°,求出∠EAD=15°,同理∠EDA=15°,最后由三角形内角和求出∠DEA的度数.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.
∵△BEC是正三角形,
∴BE=BC=EC,∠EBC=∠BEC=∠ECB=60°.
∴BA=BE(即△BAE是等腰三角形),
∠ABE=∠ABC-∠EBC= 90°-60°=30°,
∴∠BAE=∠BEA=![]() =75°,
=75°,
∴∠EAD=∠BAD-∠BAE=90°-75°=15°.
同理∠EDA=15°,
∴∠DEA=180°-∠EAD-∠EDA=180°-15°-15°=150°.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
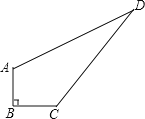
【题目】为将我们的城市装扮的更美丽,园林绿化工人要将公园一角的一块四边形的空地ABCD种植上花草.经测量,∠B=90°,AB=3米,BC=4米,CD=12米,DA=13米.若每平方米空地需要购买150元的花草.将这块空地全部绿化需要购买多少元的这种花草?
查看答案和解析>>
科目:初中数学 来源: 题型:
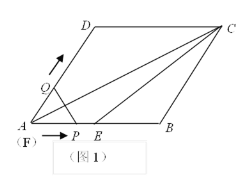
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A—D—C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
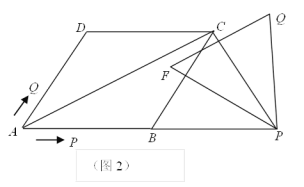
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α ° (0<α<360°),直线PF 分别与直线AC、直线CD交于点M、N.是否存在这样的α ,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
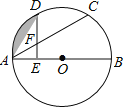
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
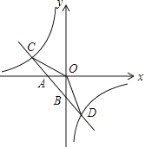
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
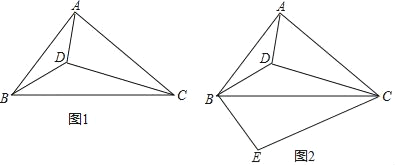
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
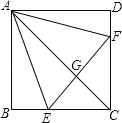
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有____.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com