
分析 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两枚骰子点数相同的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
| (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
点评 本题考查了列表法与树状图法求随机事件的概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
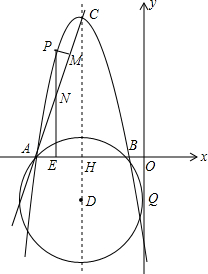 在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H
在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
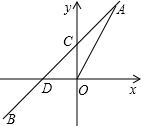 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
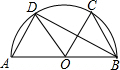 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
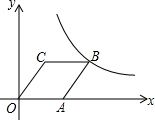 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
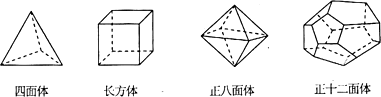
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com