
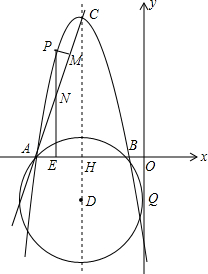
 在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H
在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H分析 (1)设抛物线的解析式为y=a(x+4)2+9.将B(-1,0)代入求得a的值即可;由抛物线的对称性求得点A的坐标,设直线AC的解析式为y=kx+b,将A(-7,0)、C(-4,9)代入求解即可;
(2)由题意可求得S△APC=3.设p(a,-a2-8a-7),N(a,3a+21).则PN=-a2-8a-7-(3a+21)=-a2-11a-28,由三角形的面积公式列出关于a的方程,然后解得a的值可求得点P的坐标;
(3)利用配方法可求得PN的最大值为$\frac{9}{4}$,然后证明△PMN∽△CHA,得到PM:MN:PN=1:3:$\sqrt{10}$,从而可求得l的最大值.
解答 解:(1)设抛物线的解析式为y=a(x+4)2+9.
∵将B(-1,0)代入得:9a+9=0,解得;a=-1,
∴解析式为y=-(x+4)2+9,即y=-x2-8x-7.
∵点A与点B关于x=-4对称,B(-1,0)
∴A(-7,0).
设直线AC的解析式为y=kx+b.
∵将A(-7,0)、C(-4,9)代入得:$\left\{\begin{array}{l}{-7k+b=0}\\{-4k+b=9}\end{array}\right.$,解得:k=3,b=21,
∴直线AC的解析式为y=3x+21.
(2)∵AH=3,CH=9,
∴S△AHC=$\frac{1}{2}×3×9$=$\frac{27}{2}$.
∵S△APC=$\frac{2}{9}{S_△}$AHC,
∴S△APC=$\frac{2}{9}$×$\frac{27}{2}$=3.
设p(a,-a2-8a-7),N(a,3a+21).则PN=-a2-8a-7-(3a+21)=-a2-11a-28.
∵S△APC=$\frac{1}{2}$PN•AH=3,
∴$\frac{1}{2}$×(-a2-11a-28)×3=3,解得:a1=-5,a2=-6.
∴点P(-5,8)或(-6,5)
(3)∵由(2)可知PN=-a2-11a-28=-(a+$\frac{11}{2}$)2+$\frac{9}{4}$.
∴PN的最大值为$\frac{9}{4}$.
∵EN∥CH,
∴∠ACH=∠ANE.
∵∠PNM=∠ENA,
∴∠PNM=∠ACH.
又∵∠PMN=∠AHC=90°,
∴△PMN∽△CHA.
∴PM:MN:PN=CH:HA:CA=1:3:$\sqrt{10}$.
∴l=PN×$\frac{1+3+\sqrt{10}}{\sqrt{10}}$=$\frac{9}{4}$×$\frac{4+\sqrt{10}}{\sqrt{10}}$=$\frac{18\sqrt{10}+45}{20}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的图象和性质、待定系数法求二次函数、一次函数的解析式、相似三角形的性质和判定、三角形的面积公式,配方法求二次函数的最值,得到PN与点P的横坐标a的函数关系式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a,请用尺规作图,并填空(不写作法,但要保留作图痕迹)
如图,已知线段a,请用尺规作图,并填空(不写作法,但要保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-30)(100-3x)=200 | B. | x(100-3x)=200 | C. | (30-x)(100-3x)=200 | D. | (x-30)(3x-100)=200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com