
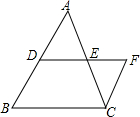
 如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?
如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?  七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:填空题
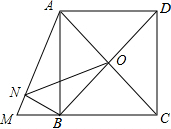 如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为$\frac{\sqrt{10}}{5}$.
如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
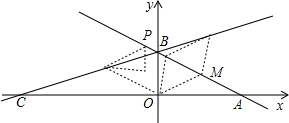 如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.
如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
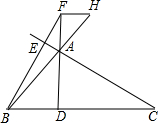 如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.
如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
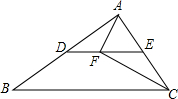 如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.
如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
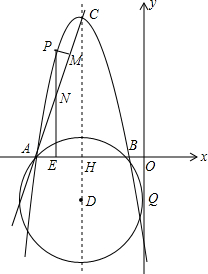 在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H
在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com