
【题目】(![]() )如图①已知四边形
)如图①已知四边形![]() 中,
中,![]() ,BC=b,
,BC=b,![]() ,求:
,求:
①对角线![]() 长度的最大值;
长度的最大值;
②四边形![]() 的最大面积;(用含
的最大面积;(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(![]() )如图②,四边形
)如图②,四边形![]() 是某市规划用地的示意图,经测量得到如下数据:
是某市规划用地的示意图,经测量得到如下数据:![]() ,
,![]() ,
,![]() ,
,![]() ,请你利用所学知识探索它的最大面积(结果保留根号)
,请你利用所学知识探索它的最大面积(结果保留根号)

【答案】(1)①![]() ;②
;②![]() ;(2)150
;(2)150![]() +475
+475![]() +475.
+475.
【解析】
(1)①由条件可知AC为直径,可知BD长度的最大值为AC的长,可求得答案;②连接AC,求得AD2+CD2,利用不等式的性质可求得ADCD的最大值,从而可求得四边形ABCD面积的最大值;
(2)连接AC,延长CB,过点A做AE⊥CB交CB的延长线于E,可先求得△ABC的面积,结合条件可求得∠D=45°,且A、C、D三点共圆,作AC、CD中垂线,交点即为圆心O,当点D与AC的距离最大时,△ACD的面积最大,AC的中垂线交圆O于点D',交AC于F,FD'即为所求最大值,再求得
△ACD′的面积即可.
(1)①因为∠B=∠D=90°,所以四边形ABCD是圆内接四边形,AC为圆的直径,则BD长度的最大值为AC,此时BD=![]() ,
,
②连接AC,则AC2=AB2+BC2=a2+b2=AD2+CD2,S△ACD=![]() ADCD≤
ADCD≤![]() (AD2+CD2)=
(AD2+CD2)=![]() (a2+b2),所以四边形ABCD的最大面积=
(a2+b2),所以四边形ABCD的最大面积=![]() (a2+b2)+
(a2+b2)+![]() ab=
ab=![]() ;
;
(2)如图,连接AC,延长CB,过点A作AE⊥CB交CB的延长线于E,因为AB=20,∠ABE=180°-∠ABC=60°,所以AE=ABsin60°=10![]() ,EB=ABcos60°=10,S△ABC=
,EB=ABcos60°=10,S△ABC=![]() AEBC=150
AEBC=150![]() ,因为BC=30,所以EC=EB+BC=40,AC=
,因为BC=30,所以EC=EB+BC=40,AC=![]() =10
=10![]() ,因为∠ABC=120°,∠BAD+∠BCD=195°,所以∠D=45°,则△ACD中,∠D为定角,对边AC为定边,所以,A、C、D点在同一个圆上,做AC、CD中垂线,交点即为圆O,如图,
,因为∠ABC=120°,∠BAD+∠BCD=195°,所以∠D=45°,则△ACD中,∠D为定角,对边AC为定边,所以,A、C、D点在同一个圆上,做AC、CD中垂线,交点即为圆O,如图,
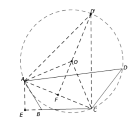
当点D与AC的距离最大时,△ACD的面积最大,AC的中垂线交圆O于点D’,交AC于F,FD’即为所求最大值,连接OA、OC,∠AOC=2∠AD’C=90°,OA=OC,所以△AOC,△AOF等腰直角三角形,AO=OD’=5![]() ,OF=AF=
,OF=AF=![]() =5
=5![]() ,D’F=5
,D’F=5![]() +5
+5![]() ,S△ACD’=
,S△ACD’=![]() ACD’F=5
ACD’F=5![]() ×(5
×(5![]() +5
+5![]() )=475
)=475![]() +475,所以Smax=S△ABC+S△ACD=150
+475,所以Smax=S△ABC+S△ACD=150![]() +475
+475![]() +475.
+475.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,且∠ABC=60°,D为△ABC内一点 ,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD=∠CBD,连DE,CE. 下列结论:①∠DAC=∠DBC;②BE⊥AC ;③∠DEB=30°. 其中正确的是( )

A.①...B.①③...C.② ...D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BC=6cm,点D为AB的中点.如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与双曲线y=![]() 交于A(2,n)、B(﹣3,﹣2)两点,与x轴,y轴分别交于C、D两点.
交于A(2,n)、B(﹣3,﹣2)两点,与x轴,y轴分别交于C、D两点.
(1)试求双曲线y=![]() 的解析式;
的解析式;
(2)试求直线y=kx+b的解析式;
(3)试求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 为对角线,点
为对角线,点![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,下列说法:
边的中点,下列说法:
①当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
②当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
③当![]() 且
且![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有_____人;
(2)补全下表中空缺的三个统计量:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 | _____ |
二班 | _____ | _____ | 90 |
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com