
【题目】某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
【答案】(1)第一次购书每本25元;(2)每本图书的售价至少是35元.
【解析】
(1)设第一次购书的进价是x元/本,则第二批每套的进价是(1+20%)x元/本,然后根据题意列出分式方程即可得出结论;
(2)设每本图书的售价为y元,然后根据题意列出不等式即可得出结论.
(1)设第一次购书的进价是x元/本,则第二批每套的进价是(1+20%)x元/本,
根据题意得:![]() =
=![]() -10,
-10,
解得:x=25,
经检验,x=25是原分式方程的解.
答:第一次购书每本25元.
(2)设每本图书的售价为y元,
根据题意得:[500÷25+(500÷25+10)]y-500-900≥(500+900)×25%,
解得:y≥35.
答:每本图书的售价至少是35元.


科目:初中数学 来源: 题型:
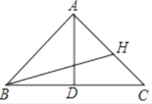
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
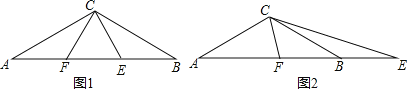
【题目】如图1,△ABC中,CA=CB,∠ACB=120°,AB=3,点E、F在直线AB上,且∠ECF=60°.
(1)求AC边的长;
(2)如图1,点E、F在线段AB上时,若EF=AF,求证:BE=EF;
(3)如图2,F在AB上,E在AB的延长线上时,AF=m,BE=n,则n= (用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: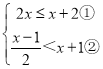
请结合题意填空,完成本题解答:
(1)解不等式①,得______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
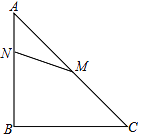
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
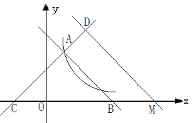
【题目】如图,直线AB:![]() 与直线AC:
与直线AC:![]() 都与双曲线
都与双曲线![]() 交于点A(1,m),这两条直线分别与
交于点A(1,m),这两条直线分别与![]() 轴交于B、C两点.
轴交于B、C两点.
(1)求![]() 和
和![]() 的值.
的值.
(2)将直线AB沿![]() 轴正方向平移,平移后交直线AC于点D,交
轴正方向平移,平移后交直线AC于点D,交![]() 轴于点M,已知M的横坐标为6,求△MCD的面积.
轴于点M,已知M的横坐标为6,求△MCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
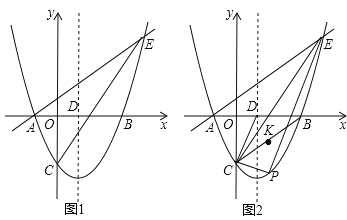
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
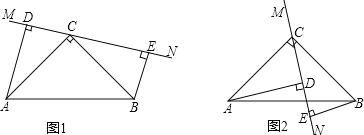
【题目】△ABC中,![]() ∠ACB=900,AC=BC,直线MN经过点C,且
∠ACB=900,AC=BC,直线MN经过点C,且![]() AD⊥MN于D,
AD⊥MN于D,![]() BE⊥MN于E.
BE⊥MN于E.
![]() 当直线MN绕点C旋转到图1的位置时,求证:
当直线MN绕点C旋转到图1的位置时,求证: ![]() ≌△CBE;②DE=AD+BE;
≌△CBE;②DE=AD+BE;
![]() 当直线MN绕点C旋转到图2的位置时,
当直线MN绕点C旋转到图2的位置时,![]() 中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com