
【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
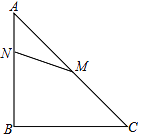
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
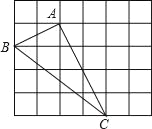
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
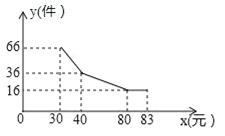
(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年暑假都是旅游旺季,某商家抓住商机,准备七、八月份力推A、B两款旅行箱,已知7月份销售10件A款旅行箱和20件B款旅行箱的总销售额为4800元,每件B款旅行箱比每件A款旅行箱的销售单价多60元。该商家在七月份A、B两款旅行箱都卖了200件.
(1)求A、B两款旅行箱的销售单价分别为多少元?
(2)八月份,A款旅行箱的销售单价在七月份的基础上上涨了0.5a%,B款旅行箱的销售单价在七月份的基础上上涨了a%,两款旅行箱的销售量都比七月份减少了![]() a%,该商家发现两款旅行箱八月份的总销售额比七月份的总销售额少3000元,求a的值.
a%,该商家发现两款旅行箱八月份的总销售额比七月份的总销售额少3000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元![]() ,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
(2)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com