
【题目】如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.
【答案】解:如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OB∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′= ![]() =
= ![]()
∴当过点P且与OB平行的直线与⊙O有公共点时,0<OP≤ ![]()
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0<OP≤ ![]()
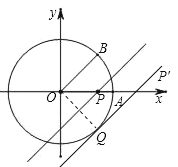
【解析】将过点P且与OB平行的直线平移至P′的位置,使其与⊙O相切,设切点为Q,连接OQ,根据条件证明△OQP′为等腰直角三角形,已知OQ=1,解直角三角形求OP′,确定OP的取值范围
【考点精析】通过灵活运用直线与圆的三种位置关系和切线的性质定理,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=![]() x+3的图象经过点B、C.
x+3的图象经过点B、C.

(1)点C的坐标为_____,点B的坐标为_____;
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图,两个反比例函数C1:y=![]() 和C2:y=
和C2:y=![]() 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点

A. ①② B. ②④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .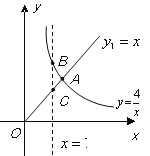
【答案】①③④
【解析】试题分析:反比例函数与一次函数的交点问题.运用一次函数和反比例函数的性质来解决的一道常见的数形结合的函数试题.一次函数和反比例函数的交点坐标就是一次函数与反比例函数组成的方程组的解.根据k>0确定一次函数和反比例函数在第一象限的图象特征来确定其增减性;根据x=1时求出点B点C的坐标从而求出BC的值;当x=2时两个函数的函数值相等时根据图象求得x>2时y1>y2.
试题解析:①由一次函数与反比例函数的解析式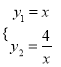 ,
,
解得, ![]() ,
,
∴A(2,2),故①正确;
②由图象得x>2时,y1>y2;故②错误;
③当x=1时,B(1,3),C(1,1),∴BC=3,故③正确;
④一次函数是增函数,y随x的增大而增大,反比例函数k>0,y随x的增大而减小.故④正确.
∴①③④正确.
考点:反比例函数与一次函数的交点问题.
【题型】填空题
【结束】
15
【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点![]() 、
、![]() 在函数
在函数![]() 的图象上,斜边
的图象上,斜边![]() 、
、![]() 都在
都在![]() 轴上,则点
轴上,则点![]() 的坐标是____________.
的坐标是____________.
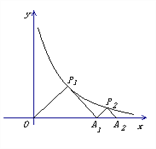
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=2AB,取AC中点D;
(2)在(1)的条件下,如果AB=4,求线段BD的长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com