
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的平衡数.
的平衡数.
![]() 与 是关于
与 是关于![]() 的平衡数,
的平衡数,![]() 与 是关于
与 是关于![]() 的平衡数. (用含
的平衡数. (用含![]() 的代数式表示)
的代数式表示)
![]() 若
若![]() ,判断
,判断![]() 与
与![]() 是否是关于
是否是关于![]() 的平衡数,并说明理由.
的平衡数,并说明理由.
【答案】(1)—1,x—3;(2)a与b不是关于1的平衡数,理由详见解析
【解析】
(1)根据平衡的定义,可得3与﹣1是关于1的平衡数,5﹣x与x﹣3是关于1的平衡数;
(2)根据平衡的定义可得a+b≠2,因此a与b不是关于1平衡数.
解:(1)设3的关于1的平衡数为a,则3+a=2,
解得a=﹣1,
∴3与﹣1是关于1的平衡数;
设5﹣x的关于1的平衡数为b,则5-x+b=2,
解得b=2-(5-x)=x-3,
∴5﹣x与x﹣3是关于1的平衡数.
(2)a与b不是关于1的平衡数.
理由如下:
∵a=2x2-3(x2+x)+4,b=2x-[3x-(4x+x2)-2],
∴a+b=2x2-3(x2+x)+4+2x-[3x-(4x+x2)-2]
=2x2-3x2-3x+4+2x-3x+4x+x2+2
=6≠2,
∴a与b不是关于1的平衡数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知A=3x2+x+2,B=﹣3x2+9x+6.
(1)求2A﹣![]() B;
B;
(2)若2A﹣![]() B与
B与![]() 互为相反数,求C的表达式;
互为相反数,求C的表达式;
(3)在(2)的条件下,若x=2是C=2x+7a的解,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
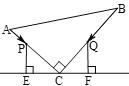
【题目】如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿![]() 路径向终点B运动,点Q从B点出发,沿
路径向终点B运动,点Q从B点出发,沿![]() 路径向终点A运动.点P 和Q分别
路径向终点A运动.点P 和Q分别![]() 和
和![]() 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的对称中心为坐标原点O,AD⊥y轴于点E(点A在点D的左侧),经过E、D两点的函数y=﹣![]() x2+mx+1(x≥0)的图象记为G1,函数y=﹣
x2+mx+1(x≥0)的图象记为G1,函数y=﹣![]() x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
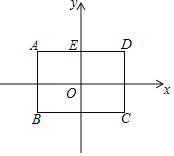
(1)当点A的横坐标为﹣1时,求m的值;
(2)求L与m之间的函数关系式;
(3)当G2与矩形ABCD恰好有两个公共点时,求L的值;
(4)设G在﹣4≤x≤2上最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出L的取值范围.
≤y0≤9时,直接写出L的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
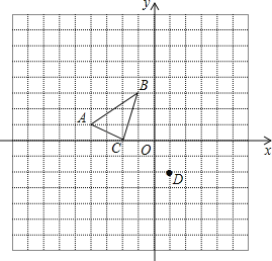
【题目】如图,三角形ABC三个顶点的坐标分别是A(-4,1),B(-1,3),C(-2,0),将三角形ABC平移得到三角形DEF,使点A与点D(1,-2)是对应点.
(1)在图中画出三角形DEF,并写出点B、C的对应点E、F的坐标;
(2)若点P在x轴上,且知三角形PCD的面积等于三角形ABC面积的![]() ,请写出满足条件的点P的坐标.
,请写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
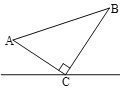
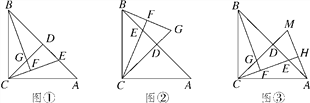
【题目】如图①,在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A,B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G.
(1)求证:AE=CG;
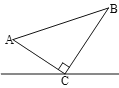
(2)若点E运动到线段BD上时(如图②),试猜想AE,CG的数量关系是否发生变化,请写出你的结论;
(3)过点A作AH⊥CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com