
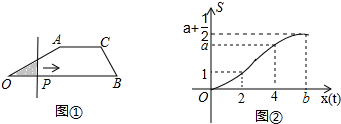
���� ��1����ͼ���У���AE��OB ��E��CF��OB��F�����ı���AECF�Ǿ��Σ���ͼ�����OE��EF��FB��AE���ɽ�����⣮
��2����ͼ���У�����������OP1=P1Aʱ����OP1=AP1=x����RT��AP1E�У����ù��ɶ������ɽ�����ڵ�OA=AP2ʱ�����ݵ������������ʼ��ɽ�����⣮
���  �⣺��1����ͼ���У���AE��OB ��E��CF��OB��F�����ı���AECF�Ǿ��Σ�
�⣺��1����ͼ���У���AE��OB ��E��CF��OB��F�����ı���AECF�Ǿ��Σ�
��ͼ��ڿ�֪��OE=2��AE=CF=1��EF=AC=4��FB=1��
��a=S��AOE+S����AECF=1+4=5��
b=OB=2+4+1=7��
��2����ͼ���У� ��OP1=P1Aʱ����OP1=AP1=x����RT��AP1E�У��ߡ�AEP1=90�㣬AE=1��AP1=x��P1E=2-x��
��OP1=P1Aʱ����OP1=AP1=x����RT��AP1E�У��ߡ�AEP1=90�㣬AE=1��AP1=x��P1E=2-x��
��x2=12+��2-x��2��
��x=$\frac{5}{4}$��
��t=$\frac{5}{4}$��
�ڵ�OA=AP2ʱ��OE=EP2=2��
��OP2=4��
��t=4��
��������t=$\frac{5}{4}$��4ʱ��OAP�ǵ��������Σ�
���� ���⿼�鶯�����⺯��ͼ���ɶ��������������ε����ʵ�֪ʶ������Ĺؼ�����ȷ��ʶͼ�ζ���ͼ����Ϣ��ѧ��������۵���ѧ˼�룬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
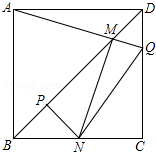 ��ͼ���߳�һ����������ABCD��QΪCD��һ�����㣬AQ��BD�ڵ�M����M��MN��AQ��BC�ڵ�N����NP��BD�ڵ�P������NQ�����н��ۣ���AM=MN����MP=$\frac{1}{2}$BD����BN+DQ=NQ����$\frac{AB+BN}{BM}$Ϊ��ֵ������һ���������Ǣ٢ڢۢܣ�
��ͼ���߳�һ����������ABCD��QΪCD��һ�����㣬AQ��BD�ڵ�M����M��MN��AQ��BC�ڵ�N����NP��BD�ڵ�P������NQ�����н��ۣ���AM=MN����MP=$\frac{1}{2}$BD����BN+DQ=NQ����$\frac{AB+BN}{BM}$Ϊ��ֵ������һ���������Ǣ٢ڢۢܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��ֱ��MN����O��A��B���㣬AC��ֱ����ADƽ�֡�CAM����O��D����D��DE��MN��E��
��֪����ͼ��ֱ��MN����O��A��B���㣬AC��ֱ����ADƽ�֡�CAM����O��D����D��DE��MN��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com