
ЁОЬтФПЁПвбжЊЃКЪ§жсЩЯгаAЁЂBЁЂCШ§ИіЕуЃЌЫќУЧБэЪОЕФЪ§ЗжБ№ЪЧaЁЂbКЭ8ЃЌOЪЧдЕуЃЌЧвЃЈa+20ЃЉ2+|b+10|ЃН0ЃЎ
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєНЋЪ§жселЕўЃЌЪЙЕУЕуAгыЕуCжиКЯЃЌдђЕуBгыЪ§ЁЁ ЁЁБэЪОЕФЕужиКЯЃЛ
ЃЈ3ЃЉЖЏЕуMдкЪ§жсЩЯдЫЖЏЃЌЪЧЗёДцдкЕуMЪЙЕУMC+MBЃН20ЃЌШєДцдкЃЌЧыЧѓГіЕуMЖдгІЕФЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЯжгаЖЏЕуPЁЂQЗжБ№ДгAЁЂBСНЕуГіЗЂЃЌЕуPвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCвЦЖЏЃЌЭЌЪБЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCвЦЖЏЃЎЩшЕуPвЦЖЏЕФЪБМфЮЊtУыЃЌЮЪЃК
ЂйЕБtЮЊЖрЩйЪБЃЌЕуPзЗЩЯЕуQЃП
ЂкгУКЌtЕФДњЪ§ЪНБэЪОЯпЖЮPQЕФГЄЖШЃП
ЁОД№АИЁПЃЈ1ЃЉЉ20ЃЛЉ10ЃЛЃЈ2ЃЉЉ2ЃЛЃЈ3ЃЉДцдкЕуMЪЙЕУMC+MBЃН20ЃЌЕуMЖдгІЕФЪ§ЮЊЉ11Лђ9ЃЎЃЈ4ЃЉЂйЕБtЮЊ5ЪБЃЌЕуPзЗЩЯЕуQЃЎЂкPQЃН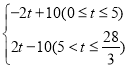 ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНЗНЪ§ЕФЗЧИКадЁЂОјЖджЕЕФЗЧИКадСаГіЕШЪНЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉгЩелЕўКѓжиКЯЕФЕуБэЪОЕФЪ§жЎКЭВЛБфЃЌЧѓНтМДПЩЕУЃЛ
ЃЈ3ЃЉЩшЕуMЖдгІЕФЪ§ЮЊ![]() ЃЌЗжЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЁЂЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЁЂЕуMдкЕуBЕФзѓВрШ§жжЧщаЮЃЌИљОн
ЃЌЗжЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЁЂЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЁЂЕуMдкЕуBЕФзѓВрШ§жжЧщаЮЃЌИљОн![]() СаГіЕШЪНЧѓНтМДПЩЃЛ
СаГіЕШЪНЧѓНтМДПЩЃЛ
ЃЈ4ЃЉИљОнЬтвтЕУЃЌЕуPБэЪОЕФЪ§ЮЊ![]() ЃЌЕуQБэЪОЕФЪ§ЮЊ
ЃЌЕуQБэЪОЕФЪ§ЮЊ![]()
ЂйЕуPзЗЩЯЕуQЃЌдђЕуPБэЪОЕФЪ§ЕШгкЕуQБэЪОЕФЪ§ЃЌСаГіЕШЪНЧѓНтМДПЩЃЛ
ЂкгЩЬтЂйПЩжЊЃЌЕуPзЗЩЯЕуQЪБЃЌЛЙЮДЕНДяЕуCЃЌЫљвдЗжСНжжЧщПіЃКдкЕуPзЗЩЯЕуQжЎЧАЁЂдкЕуPзЗЩЯЕуQжЎКѓжСЕНДяЕуCЃЌЗжБ№РћгУЕуPЁЂQДњБэЕФЪ§зїВюМДПЩ.
ЃЈ1ЃЉ![]()
гЩЦНЗНЪ§ЕФЗЧИКадЁЂОјЖджЕЕФЗЧИКадЕУ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩелЕўКѓжиКЯЕФЕуБэЪОЕФЪ§жЎКЭВЛБфПЩЕУЃК![]()
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшЕуMЖдгІЕФЪ§ЮЊ![]() ЃЌгЩЬтвтЗжвдЯТШ§жжЧщаЮЃК
ЃЌгЩЬтвтЗжвдЯТШ§жжЧщаЮЃК
ЂйЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЃЌДЫЪБ![]()
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЗћКЯ
ЃЌЗћКЯ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ЂкЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЃЌДЫЪБ![]()
дђ![]() ЃЌЗНГЬЮоНт
ЃЌЗНГЬЮоНт
ЂлЕуMдкЕуBЕФзѓВрЃЌДЫЪБ![]()
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЗћКЯ
ЃЌЗћКЯ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ЙЪДцдкетбљЕФЕуMЪЙЕУ![]() ЃЌЕуMЖдгІЕФЪ§ЮЊ
ЃЌЕуMЖдгІЕФЪ§ЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉгЩЬтвтЕУЃЌЕуPБэЪОЕФЪ§ЮЊ![]() ЃЌЕуQБэЪОЕФЪ§ЮЊ
ЃЌЕуQБэЪОЕФЪ§ЮЊ![]()
ЂйЕуPзЗЩЯЕуQЃЌдђ![]()
НтЕУЃК![]()
Д№ЃКЕБtЮЊ5ЪБЃЌЕуPзЗЩЯЕуQЃЛ
ЂкгЩЬтвтЕУЃЌЕуPЯШзЗИЯЕуQЃЌзЗЩЯКѓЛсЯШЕНДяЕуC
ЕуPЕНДяЕуCЪБЃЌЕуPвЦЖЏЕФЪБМф![]() ЮЊЃК
ЮЊЃК![]() ЃЌМД
ЃЌМД![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
злЩЯЃЌ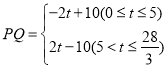 .
.


 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСНЬѕжБЯпABЃЌCDЯрНЛгкЕуOЃЌЧвЁЯAOCЃНЁЯAODЃЌЩфЯпOMДгOBПЊЪМШЦOЕуФцЪБеыЗНЯђа§зЊЃЌЫйЖШЮЊ15Ёу/sЃЌЩфЯпONЭЌЪБДгODПЊЪМШЦOЕуЫГЪБеыЗНЯђа§зЊЃЌЫйЖШЮЊ12Ёу/sЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЃМ12ЃЌБОЬтГіЯжЕФНЧОљаЁгкЦННЧЃЉ
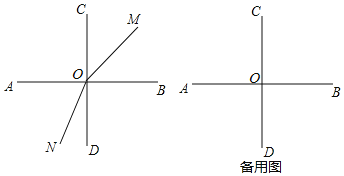
ЃЈ1ЃЉЭМжавЛЖЈгаЁЁ ЁЁИіжБНЧЃЛЕБtЃН2ЪБЃЌЁЯMONЕФЖШЪ§ЮЊЁЁ ЁЁЃЌЁЯBONЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєOEЦНЗжЁЯCOMЃЌOFЦНЗжЁЯNODЃЌЕБЁЯEOFЮЊжБНЧЪБЃЌЧыЧѓГіtЕФжЕЃЛ
ЃЈ3ЃЉЕБЩфЯпOMдкЁЯCOBФкВПЃЌЧв![]() ЪЧЖЈжЕЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіетИіЖЈжЕЃЎ
ЪЧЖЈжЕЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіетИіЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЦНУцжБНЧзјБъЯЕжаСНЖЈЕуAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпy=ax2+bxЉ2ЃЈaЁй0ЃЉЙ§ЕуAЃЌBЃЌЖЅЕуЮЊCЃЌЕуPЃЈmЃЌnЃЉЃЈnЃМ0ЃЉЮЊХзЮяЯпЩЯвЛЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕБЁЯAPBЮЊЖлНЧЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєmЃО![]() ЃЌЕБЁЯAPBЮЊжБНЧЪБЃЌНЋИУХзЮяЯпЯђзѓЛђЯђгвЦНвЦtЃЈ0ЃМtЃМ
ЃЌЕБЁЯAPBЮЊжБНЧЪБЃЌНЋИУХзЮяЯпЯђзѓЛђЯђгвЦНвЦtЃЈ0ЃМtЃМ![]() ЃЉИіЕЅЮЛЃЌЕуCЁЂPЦНвЦКѓЖдгІЕФЕуЗжБ№МЧЮЊCЁфЁЂPЁфЃЌЪЧЗёДцдкtЃЌЪЙЕУЪзЮЛвРДЮСЌНгAЁЂBЁЂPЁфЁЂCЁфЫљЙЙГЩЕФЖрБпаЮЕФжмГЄзюЖЬЃПШєДцдкЃЌЧѓtЕФжЕВЂЫЕУїХзЮяЯпЦНвЦЕФЗНЯђЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЉИіЕЅЮЛЃЌЕуCЁЂPЦНвЦКѓЖдгІЕФЕуЗжБ№МЧЮЊCЁфЁЂPЁфЃЌЪЧЗёДцдкtЃЌЪЙЕУЪзЮЛвРДЮСЌНгAЁЂBЁЂPЁфЁЂCЁфЫљЙЙГЩЕФЖрБпаЮЕФжмГЄзюЖЬЃПШєДцдкЃЌЧѓtЕФжЕВЂЫЕУїХзЮяЯпЦНвЦЕФЗНЯђЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
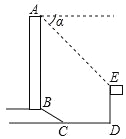
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГАьЙЋДѓТЅе§ЧАЗНгавЛИљИпЖШЪЧ15УзЕФЦьИЫEDЃЌДгАьЙЋДѓТЅЖЅЖЫAВтЕУЦьИЫЖЅЖЫEЕФИЉНЧІСЪЧ45ЁуЃЌЦьИЫЕЭЖЫDЕНДѓТЅЧАЬнПГЕзБпЕФОрРыDCЪЧ20УзЃЌЬнПВЦТГЄBCЪЧ12УзЃЌЬнПВЦТЖШi=1:![]() ЃЌдђДѓТЅABЕФИпЖШЮЊ_________УзЃЎ
ЃЌдђДѓТЅABЕФИпЖШЮЊ_________УзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКдке§ЗНаЮABCDжаЃЌEЮЊCDБпЩЯЕФвЛЕуЃЌFЮЊBCЕФбгГЄЯпЩЯвЛЕуЃЌCEЃНCFЁЃ
ЂХЁїBCEгыЁїDCFШЋЕШТ№ЃПЫЕУїРэгЩЃЛ
ЂЦШєЁЯBECЃН60oЃЌЧѓЁЯEFDЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫГДЮСЌНгвЛИіЫФБпаЮЕФИїБпжаЕуЃЌЕУЕНСЫвЛИіОиаЮЃЌдђЯТСаЫФБпаЮжаТњзуЬѕМўЕФЪЧЃЈЁЁЁЁЃЉ
ЂйЦНааЫФБпаЮЃЛЂкСтаЮЃЛЂлОиаЮЃЛЂмЖдНЧЯпЛЅЯрДЙжБЕФЫФБпаЮЃЎ
A. ЂйЂлB. ЂкЂлC. ЂлЂмD. ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЕФзјБъЮЊЃЈЉ![]() ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧѓЙ§AЃЌBСНЕужБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЙ§BЕузїжБЯпBPгыxжсНЛгкЕуPЃЌЧвЪЙOP=2OAЃЌЧѓЁїABPЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЧщОГЃК
ЦНУцжБНЧзјБъЯЕжаЃЌОиаЮжНЦЌOBCDАДШчЭМЕФЗНЪНЗХжУ![]() вбжЊ
вбжЊ![]() ЃЌ
ЃЌ![]() ЃЌНЋетеХжНЦЌбиЙ§ЕуBЕФжБ
ЃЌНЋетеХжНЦЌбиЙ§ЕуBЕФжБ
ЯпелЕўЃЌЪЙЕуOТфдкБпCDЩЯЃЌМЧзїЕуAЃЌелКлгыБпODНЛгкЕуEЃЎ
Ъ§бЇЬНОПЃК
![]() ЕуCЕФзјБъЮЊ______ЃЛ
ЕуCЕФзјБъЮЊ______ЃЛ
![]() ЧѓЕуEЕФзјБъМАжБЯпBEЕФКЏЪ§ЙиЯЕЪНЃЛ
ЧѓЕуEЕФзјБъМАжБЯпBEЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ШєЕуPЪЧxжсЩЯЕФвЛЕуЃЌжБЯпBEЩЯЪЧЗёДцдкЕуQЃЌФмЪЙвдAЃЌBЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃП
ШєЕуPЪЧxжсЩЯЕФвЛЕуЃЌжБЯпBEЩЯЪЧЗёДцдкЕуQЃЌФмЪЙвдAЃЌBЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃП
ШєДцдкЃЌжБНгаДГіЯргІЕФЕуQЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCЪЧвЛПщКЌга45ЕФжБНЧШ§НЧАхЃЌЫФБпаЮDEFGЪЧГЄЗНаЮЃЌDЁЂGЗжБ№дкABЁЂACЩЯЃЌEЁЂFдкBCЩЯЁЃBC=16,DG=4ЃЌDE=6ЃЌЯжНЋГЄЗНаЮ DEFGЯђгвбиBCЗНЯђЦНвЦЃЌЩшЫЎЦНвЦЖЏЕФОрРыЮЊdЃЌГЄЗНаЮгыжБНЧШ§НЧАхЕФжиЕўУцЛ§ЮЊSЃЌ
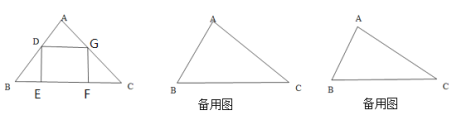
ЃЈ1ЃЉЕБЫЎЦНОрРыdЪЧКЮжЕЪБЃЌГЄЗНаЮ DEFGЧЁКУЭъШЋвЦГіШ§НЧАхЃЛ
ЃЈ2ЃЉдквЦЖЏЙ§ГЬжаЃЌЧыФугУКЌгаdЕФДњЪ§ЪНБэЪОжиЕўУцЛ§SЃЌВЂаДГіЯргІЕФdЕФЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com