
����Ŀ����ABC��һ�麬��45��ֱ�����ǰ壬�ı���DEFG�dz����Σ�D��G�ֱ���AB��AC�ϣ�E��F��BC�ϡ�BC=16,DG=4��DE=6���ֽ������� DEFG������BC����ƽ�ƣ���ˮƽ�ƶ��ľ���Ϊd����������ֱ�����ǰ���ص����ΪS��
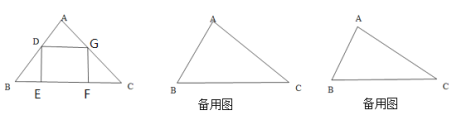
��1����ˮƽ����d�Ǻ�ֵʱ�������� DEFGǡ����ȫ�Ƴ����ǰ壻
��2�����ƶ������У������ú���d�Ĵ���ʽ��ʾ�ص����S����д����Ӧ��d�ķ�Χ��
���𰸡���1��10����2����0<d��4ʱ��S=24-![]() ����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=
����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=![]() ����10<dʱ,S=0.
����10<dʱ,S=0.
��������
��1��Ҫʹ��������ȫ�Ƴ������Eƽ�Ƶ��˵�C������ʱd=EC���ɵ���ֱ�������ε����ʿ�֪��B=45�����Ӷ��õ�BE=DE=6.���ü���BC-BE��ֵ����.
��2��������������λ���ͼ�Σ��ٽ��ͼ�ν��м��㼴��.
�⣺��1������ABC�ǵ���ֱ�������Σ�
���B=��C=45.
���ı���DEFG�dz����Σ�
���DEF=��GFE=90��.
�ߡ�DEF+��BED=180��.
���BED=90��.
��BE=DE=6.
��BE+CE=BC=16,
��CE= BC-BE=16-6=10.
�൱ˮƽ����d��10ʱ�������� DEFGǡ����ȫ�Ƴ����ǰ壻
(2)�ٵ�0<d��4ʱ����ͼ1��ʾ��
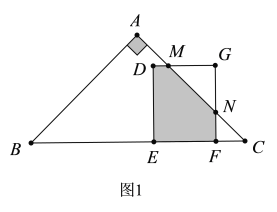
�ߡ�GNM=��FNC=��C=45������G=90����
��GN=GM=d.
��S=������DEFG�����-��GMN�����
=24-![]() ��
��
�ڵ�4<d��6ʱ����ͼ2��ʾ��
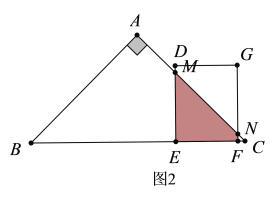
�������֪��BE=6+d,FC=6-d.
��BC=16,
��EC=16-BE=10-d.
�ߡ�C=45����
��ME= EC =10-d.FN= FC=6-d.
��S=��MEC���-��FCN�����
=![]()
=![]() ��10-d+6-d��(10-d-6+d)
��10-d+6-d��(10-d-6+d)
=32-4d.
�۵�6<d��10ʱ����ͼ2��ʾ��
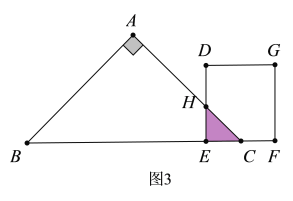
��EH=EC=10-d
��S=![]()
=![]()
�ܵ�10<dʱ,������DEFG����ABCû���ص����֣�
��S=0.
������������0<d��4ʱ��S=24-![]() ����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=
����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=![]() ����10<dʱ,S=0.
����10<dʱ,S=0.


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��B��C�����㣬���DZ�ʾ�����ֱ���a��b��8��O��ԭ�㣬�ң�a+20��2+|b+10|��0��
��1����գ�a���� ����b���� ����
��2�����������۵���ʹ�õ�A���C�غϣ����B������ ����ʾ�ĵ��غϣ�
��3������M���������˶����Ƿ���ڵ�Mʹ��MC+MB��20�������ڣ��������M��Ӧ�������������ڣ���˵�����ɣ�
��4�����ж���P��Q�ֱ��A��B�����������P��ÿ��3����λ���ȵ��ٶ����C�ƶ���ͬʱ��Q��ÿ��1����λ���ȵ��ٶ����C�ƶ������P�ƶ���ʱ��Ϊt�룬�ʣ�
�ٵ�tΪ����ʱ����P�ϵ�Q��
���ú�t�Ĵ���ʽ��ʾ�߶�PQ�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
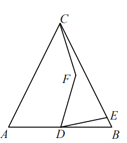
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�D��AB�е㣬E�DZ�BC��һ���㣬����DE����DE�Ƶ�D��ʱ����ת60����DF������CF����CF=![]() ����BE=_________��
����BE=_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƶ�֧����ݸ�Ч���й��ƶ�֧�������紦������ˮƽ��Ϊ�˽�����ƽʱ��ϲ�������֣��ƶ�֧��֧����ʽ��Ϊ����ij���н֣�ʹ��ij����������ʹ���ƶ�֧�������˽�������������飬�������ĸ�ѡ�֧�������ţ����п��������ƶ�֧����ÿ��ֻѡһ��)�������Ǹ��ݵ������ֱ������IJ�����������ͳ��ͼ������ͳ��ͼ.
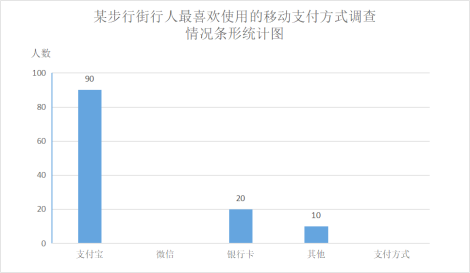

�����������ͳ��ͼ�ṩ����Ϣ,�����������.
(1)����������������� ;
(2)�벹ȫ����ͳ��ͼ;
(3)���ڴ˴ε����б�ʾʹ����֧�����������Ե�Բ�ĽǵĶ���.
(4)��ij��ò��н�������Ϊ10���ˣ�����40%���˹��ﲢѡ���ƶ�֧�����������ݴ˴ε����õ���Ϣ������һ�µ���ʹ�����п�֧��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������̶ӳа��˵���ij���ȫ��3900��ʩ�����ֱ���ϣ�����������ͬʱ��ǰ�������֪���̶ӱ��ҹ��̶�ƽ��ÿ�����0.4����13���ʩ���������̶ӹ������156��.
(1)��ף����������̶�ƽ��ÿ�����������ף�
(2)Ϊ�ӿ칤�̽��������̶Ӷ��Ľ���ʩ����������ʣ��Ĺ����У����̶�ƽ��ÿ���ܱ�ԭ������0.4�ף��ҹ��̶�ƽ��ÿ���ܱ�ԭ������0.6�ף�����ʩ�������ܹ���ԭ�����ö�������������أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ҵ�ס�����ͽṹͼ�����ݽṹͼ�ṩ����Ϣ������������⣺
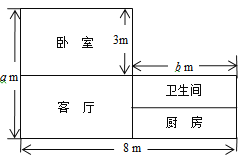
��1���ú�a��b�Ĵ���ʽ��ʾС���ҵ�ס�������S��
��2��С���������������������ש�����������õĵ�ש�۸�Ϊÿƽ����50Ԫ�������䡢�����Ϳ������õĵ�ש�۸�Ϊÿƽ����40Ԫ�����ú�a��b�Ĵ���ʽ��ʾ�����ש���ܷ���W��
��3���ڣ�2���������£���a��6��b��4ʱ����W��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��С���ڽ�ѧ¥�����9�ߵĴ���C���������ǰ����˶���A�������Ϊ37������˵ײ�B��ĸ���Ϊ45��������ʱ�������϶������ھ����2.25�״����������������ȽȽ���𣬲��ڹ��貥��45�����ʱ������˶��ˣ������Ӧ�Զ�����/����ٶ��������������ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A�ں��й����У����ֵ���B������ƫ��60���ķ����ϣ�����C������ƫ��30�������ϣ������н��ۣ��١�NAB��60�����ڡ�WAC��120������ͼ�С�NAC�IJ������������ֱ��ǡ�SAC�͡�EAB����ͼ����4�Ի���Ľǣ�������ȷ�ĸ����У�������
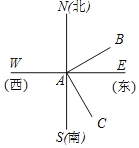
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��д�������
��1������3��4���� ����
��2��|��![]() |���� ����
|���� ����
��3����9+5���� ����
��4����12+32���� ����
��5����8��3���� ����
��6������2��3��0.25��0���� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com