
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩,测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
(1)小明将三人的成绩整理后制作了下面的表格:
平均数 | 中位数 | 众数 | 方差 | |
甲 | 7 | b | 7 | 0.8 |
乙 | 7 | 7 | d | 0.4 |
丙 | a | c | e | 0.81 |
则表中a= ,b= ,c= ,d= ,e= .
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请作出简要分析.
【答案】(1)6.3,7,6,7,6;(2)选乙运动员更合适.
【解析】
(1)根据平均数、中位数、众数的定义进行计算即可.(2)根据平均数、中位数、众数接近,方差越小,数据波动越小,成绩越优秀进行判断即可.
(1)运动员甲测试成绩按从小到大的顺序排列为:5,6,7,7,7,7,7,8,8,8,所以中位数b=(7+7)÷2=7.
运动员乙测试成绩中,数据7出现了5次,次数最多,所以众数d=7.
运动员丙测试成绩的平均数为a=![]() (2×5+4×6+3×7+1×8)=6.3,中位数c=(6+6)÷2=6,众数e=6;
(2×5+4×6+3×7+1×8)=6.3,中位数c=(6+6)÷2=6,众数e=6;
故答案是:6.3,7,6,7,6;
(2)∵甲、乙、丙三人的众数为7;7;6,
甲、乙、丙三人的中位数为7;7;6,![]()
甲、乙、丙三人的平均数为7;7;6.3,
∴甲、乙比丙优秀一些,
∵S甲2>S乙2,
∴选乙运动员更合适.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B. F. C.E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,
(1)若x12+x22=6,求m值;
(2)令T=![]() ,求T的取值范围.
,求T的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,E为AB的中点,G为BC延长线上一点,射线EO与∠ACG的角平分线交于点F,若AB=8,BC=6,则线段EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
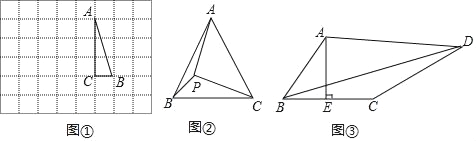
(1)请按要求画图:将△ABC绕点A按逆时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′
(2)在(1)所画图形中,∠AB′B= .
(问题解决)
如图②,在等边三角形ABC中,AC=![]() ,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找线段PA、PC之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找线段PA、PC之间的数量关系;
请参考小明同学的想法,完成该问题的解答过程.(求解一种方法即可)
(灵活运用)
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),直接写出BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.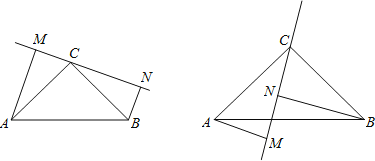
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,线段
,线段![]() 上有动点
上有动点![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 边于点
边于点![]() ,并使得
,并使得![]() .
.
![]() 当
当![]() 与
与![]() 重合时,求
重合时,求![]() 的长;
的长;
![]() 在直线
在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 的边长为
的边长为![]() 厘米,对角线
厘米,对角线![]() 上的两个动点
上的两个动点![]() ,
,![]() .点
.点![]() 从点
从点![]() ,点
,点![]() 从点
从点![]() 同时出发,沿对角线以
同时出发,沿对角线以![]() 厘米/秒的相同速度运动,过
厘米/秒的相同速度运动,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,过
,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形面积为
围成的图形面积为![]() ,
,![]() ,
,![]() ,
,![]() 围成的图形面积为
围成的图形面积为![]() (这里规定:线段的面积为
(这里规定:线段的面积为![]() 到达
到达![]() ,
,![]() 到达
到达![]() 停止.若
停止.若![]() 的运动时间为
的运动时间为![]() 秒,解答下列问题:
秒,解答下列问题:

![]() 如图,判断四边形
如图,判断四边形![]() 是什么四边形,并证明;
是什么四边形,并证明;
![]() 当
当![]() 时,求
时,求![]() 为何值时,
为何值时,![]() ;
;
![]() 若
若![]() 是
是![]() 与
与![]() 的和,试用
的和,试用![]() 的代数式表示
的代数式表示![]() .(如图为备用图)
.(如图为备用图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com