
����Ŀ�����������֣�
��ͼ�٣��ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���ABC������������ڸ���ϣ�
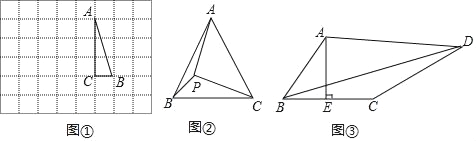
��1���밴Ҫ��ͼ������ABC�Ƶ�A����ʱ�뷽����ת90������B�Ķ�Ӧ��ΪB������C�Ķ�Ӧ��ΪC��������BB��
��2���ڣ�1������ͼ���У���AB��B=�� ����
����������
��ͼ�ڣ��ڵȱ�������ABC�У�AC=![]() ����P�ڡ�ABC�ڣ��ҡ�APC=90�㣬��BPC=120�������APC�������
����P�ڡ�ABC�ڣ��ҡ�APC=90�㣬��BPC=120�������APC�������
С��ͬѧͨ���۲졢������˼���������������γ��������뷨��
�뷨һ������APC�Ƶ�A��˳ʱ�뷽����ת60�����õ���AP��B������PP����Ѱ���߶�PA��PC֮���������ϵ��
�뷨��������APB�Ƶ�A����ʱ�뷽����ת60�����õ���AP��C��������PP����Ѱ���߶�PA��PC֮���������ϵ��
��ο�С��ͬѧ���뷨����ɸ�����Ľ����̣������һ�ַ������ɣ�
��������ã�
��ͼ�ۣ����ı���ABCD�У�AE��BC������ΪE����BAE=��ADC��BE=CE=2��CD=5��AD=kAB��kΪ��������ֱ��д��BD�ij����ú�k��ʽ�ӱ�ʾ����
���𰸡����������֡���1����ͼ����������2��45��������������S��APC=![]() ����������á�BD=
����������á�BD=![]() ��
��
��������
��1��������ת�ǣ���ת����ͼ�μ��ɣ���2��ֻҪ֤����ABB���ǵ���ֱ�������μ��ɣ�������������ͼ�ڣ�����APB�Ƶ�A����ʱ�뷽����ת60�����õ���AP��C����֤����PP��C=90�������ù��ɶ������ɵó���. ��������á���ͼ���У���AE��BC��BE=EC���Ƴ�AB=AC������ABD�Ƶ�A��ʱ����ת�õ���ACG������DG����BD=CG��ֻҪ֤����GDC=90�����ɵ�CG=![]() ���ɴ˼��ɽ�����⣻
���ɴ˼��ɽ�����⣻
��1����ͼ��ʾ����AB��C����Ϊ����

��2������BB��������ABC�Ƶ�A��˳ʱ�뷽����ת90�㣬
��AB=AB�䣬��B��AB=90�㣬
���AB��B=45�㣬
�ʴ�Ϊ��45�㣻
����������
��ͼ����
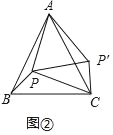
�߽���APB�Ƶ�A����ʱ�뷽����ת60�����õ���AP��C�䣬
���APP���ǵȱ������Σ���AP��C=��APB=360�㩁90�㩁120��=150�㣬
��PP��=AP����AP��P=��APP��=60�㣬
���PP��C=90�㣬��P��PC=30�㣬
��PP��=![]() PC����AP=
PC����AP=![]() PC��
PC��
�ߡ�APC=90�㣬
��AP2+PC2=AC2������![]() PC��2+PC2=
PC��2+PC2=![]()
��PC=2��
��AP=![]() ��
��
��S��APC=![]() APPC=
APPC=![]() ��
��![]() ��2=
��2=![]() ��
��
��������á�
��ͼ���У���AE��BC��BE=EC��
��AB=AC������ABD�Ƶ�A��ʱ����ת�õ���ACG������DG����BD=CG��
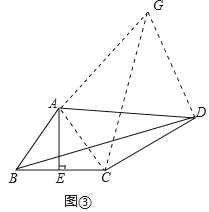
�ߡ�BAD=��CAG��
���BAC=��DAG��
��AB=AC��AD=AG��
���ABC=��ACB=��ADG=��AGD��
���ABC�ס�ADG��
��AD=kAB��
��DG=kBC=4k��
�ߡ�BAE+��ABC=90�㣬��BAE=��ADC��
���ADG+��ADC=90�㣬
���GDC=90�㣬
��CG=![]() =
=![]() ��
��
��BD=CG=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣬�г�һԪ���η��̣������仯��һ����ʽ��
![]() ij����
ij����![]() ��ͬѧ����ҵʱ�����Լ�����Ƭ��ȫ������ͬѧ����һ�ű�ʾ���ȫ���
��ͬѧ����ҵʱ�����Լ�����Ƭ��ȫ������ͬѧ����һ�ű�ʾ���ȫ���![]() ����Ƭ��
����Ƭ��
![]() һ�������Ϊ
һ�������Ϊ![]() �����ȿ���
�����ȿ���![]() ����������εij������
����������εij������
![]() ��һ�����Ϊ
��һ�����Ϊ![]() �ij�����ֽƬ��һ����
�ij�����ֽƬ��һ����![]() ����һ����
����һ����![]() ��ǡ�ñ��һ�������Σ�����������εı߳���
��ǡ�ñ��һ�������Σ�����������εı߳���
![]() һ��ֱ�������ε�б�߳���
һ��ֱ�������ε�б�߳���![]() ����ֱ�DZ�֮��Ϊ
����ֱ�DZ�֮��Ϊ![]() ����϶�ֱ�DZ߳���
����϶�ֱ�DZ߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�鳤�Ϳ��ֱ�Ϊ60����40���ij�������Ƥ��Ҫ�������Ľǽ�ȥ�ĸ���ȵ�С�����Σ��۳�һ���ǵij�����ˮ�ۣ�ʹ���ĵ����Ϊ800ƽ������.���ȥ�����εı߳�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+5��˫����![]() ��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC�������
��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC�������![]() ������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����
������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����![]() ��x��0���Ľ����У� ��
��x��0���Ľ����У� ��

A. 0��B. 1��C. 2��D. 0������1������2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
�˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
��1��С�������˵ijɼ�����������������ı���
ƽ���� | ��λ�� | ���� | ���� | |
�� | 7 | b | 7 | 0.8 |
�� | 7 | 7 | d | 0.4 |
�� | a | c | e | 0.81 |
�����a=�� ����b=�� ����c=�� ��d=�� ����e=�� ����
��2����������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭�����ʣ���������Ҫ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DE��AB��E��DF��AC��F����BD��CD��BE��CF�������н��ۣ���DE��DF����ADƽ�֡�BAC����AE��AD����AC��AB��2BE����ȷ����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ��������˵������ȷ���ǣ� ��
��ͼ����ͼ��ʾ��������˵������ȷ���ǣ� ��

A. ![]() B.
B. ![]()
C. ��![]() ʱ��
ʱ��![]() ��
��![]() ���������С D.
���������С D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��x3x4x5
��2��![]() ��
��
��3������2mn2��2��4mn3��mn+1����
��4��3a2��a3b2��2a����4a����a2b��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���ACB=90�㣬��ABC�Ľ�ƽ����AD��BE�ཻ�ڵ�P����P��PF��AD��BC���ӳ����ڵ�F����AC�ڵ�H�������н��ۣ��١�APB=135�㣻��BF=BA����PH=PD��������CP��CPƽ�֡�ACB��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com