
【题目】根据下列问题,列出一元二次方程,并将其化成一般形式:
![]() 某班有
某班有![]() 名同学,毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送
名同学,毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送![]() 张照片.
张照片.
![]() 一矩形面积为
一矩形面积为![]() ,长比宽多
,长比宽多![]() ,求这个矩形的长与宽.
,求这个矩形的长与宽.
![]() 把一块面积为
把一块面积为![]() 的长方形纸片的一边剪下
的长方形纸片的一边剪下![]() ,另一边剪下
,另一边剪下![]() ,恰好变成一个正方形,求这个正方形的边长.
,恰好变成一个正方形,求这个正方形的边长.
![]() 一个直角三角形的斜边长是
一个直角三角形的斜边长是![]() ,两直角边之差为
,两直角边之差为![]() ,求较短直角边长.
,求较短直角边长.
【答案】![]()
![]() ;
;![]() ;
;![]()
![]() ;
;![]() .
.
【解析】
(1)如果全班有![]() 名同学,那么每名同学要送出
名同学,那么每名同学要送出![]() 张;那么总共送的张数应该是
张;那么总共送的张数应该是![]() 张,即可列出方程;
张,即可列出方程;
(2)分别表示出矩形的长和宽,利用面积公式列出方程即可;
(3)设正方形的边长是![]() ,则原长方形的长为
,则原长方形的长为![]() ,原长方形的宽为
,原长方形的宽为![]() ,由长方形的面积解答即可;
,由长方形的面积解答即可;
(4)设出较短直角边,然后表示出较长直角边,然后根据勾股定理列出方程即可.
![]() ∵全班有
∵全班有![]() 名同学,
名同学,
∴每名同学要送出![]() 张;
张;
又∵是互送照片,
∴总共送的张数应该是![]() ,
,
化为一般形式为![]() ;
;
![]() 设矩形的宽为
设矩形的宽为![]() ,则长为
,则长为![]() ,
,
根据题意得:![]() ,
,
化为一般形式为:![]() ;
;
![]() 设正方形的边长是
设正方形的边长是![]() ,则原长方形的长为
,则原长方形的长为![]() ,原长方形的宽为
,原长方形的宽为![]() ,根据题意列方程得,
,根据题意列方程得,
![]() ,
,
化为一般形式为:![]() ;
;
![]() 设较短直角边长为
设较短直角边长为![]() ,则较长直角长为
,则较长直角长为![]() ,
,
根据题意得:![]() ,
,
化为一般形式为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价
元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,若商场平均每天要盈利
件,若商场平均每天要盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,直线AB交
中,直线AB交![]() 轴于A(2,0),交
轴于A(2,0),交![]() 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
(1)求△ABC的面积.
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标.
(3)如图,D是第三象限内一动点,直线BE⊥CD于E, OF⊥OD交BE延长线于F.当D点运动时,![]() 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒1 cm的速度沿折线
出发,以每秒1 cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒(
秒(![]() >0).
>0).

(1)若点![]() 在
在![]() 上,且满足
上,且满足![]() ,求此时
,求此时![]() 的值;
的值;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值;
的值;
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上任意的点(不与端点重合),且
上任意的点(不与端点重合),且![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() .给出如下几个结论:①
.给出如下几个结论:①![]() ;②
;②![]() ;③
;③![]() 与
与![]() 一定不垂直;④
一定不垂直;④![]() 的大小为定值.其中正确的结论有________.
的大小为定值.其中正确的结论有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
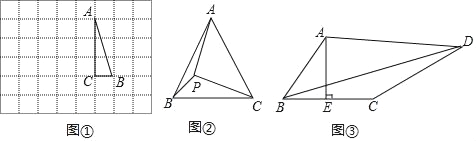
(1)请按要求画图:将△ABC绕点A按逆时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′
(2)在(1)所画图形中,∠AB′B= .
(问题解决)
如图②,在等边三角形ABC中,AC=![]() ,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找线段PA、PC之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找线段PA、PC之间的数量关系;
请参考小明同学的想法,完成该问题的解答过程.(求解一种方法即可)
(灵活运用)
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),直接写出BD的长(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com