
【题目】已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.

(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
【答案】(1)见解析;(2)∠EDH=45°;(3)EH=10![]() .
.
【解析】
(1)根据全等三角形的判定得出△CAE≌△ABD,进而利用全等三角形的性质得出AE=BD即可;
(2)根据全等三角形的判定得出△AEH≌△BDH,进而利用全等三角形的性质解答即可;
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,根据全等三角形判定和性质解答即可.
证明:(1)∵CE⊥AE,BD⊥AE,
∴∠AEC=∠ADB=90°,
∵∠BAC=90°,
∴∠ACE+CAE=∠CAE+∠BAD=90°,
∴∠ACE=∠BAD,
在△CAE与△ABD中

∴△CAE≌△ABD(AAS),
∴AE=BD;
(2)连接AH
∵AB=AC,BH=CH,
∴∠BAH=![]() ,∠AHB=90°,
,∠AHB=90°,
∴∠ABH=∠BAH=45°,
∴AH=BH,
∵∠EAH=∠BAH﹣∠BAD=45°﹣∠BAD,
∠DBH=180°﹣∠ADB﹣∠BAD﹣∠ABH=45°﹣∠BAD,
∴∠EAH=∠DBH,
在△AEH与△BDH中

∴△AEH≌△BDH(SAS),
∴EH=DH,∠AHE=∠BHD,
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°,
∴∠EDH=∠DEH=![]() ;
;
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,交HR的延长线于点T.
∵DG⊥FH,ER⊥FH,
∴∠DGH=∠ERH=90°,
∴∠HDG+∠DHG=90°
∵∠DHE=90°,
∴∠EHR+∠DHG=90°,
∴∠HDG=∠HER
在△DHG与△HER中
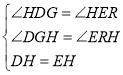
∴△DHG≌△HER (AAS),
∴HG=ER,
∵ET∥BC,
∴∠ETF=∠BHG,∠EHB=∠HET,
∠ETF=∠FHM,
∵∠EHB=∠BHG,
∴∠HET=∠ETF,
∴HE=HT,
在△EFT与△MFH中
 ,
,
∴△EFT≌△MFH(AAS),
∴HF=FT,
∴![]() ,
,
∴ER=MS,
∴HG=ER=MS,
设GH=6k,FH=5k,则HG=ER=MS=6k,
![]() ,
,
k=![]() ,
,
∴FH=5![]() ,
,
∴HE=HT=2HF=10![]() .
.



科目:初中数学 来源: 题型:
【题目】如图所示,三角形![]() (记作
(记作![]() )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是![]() ,
,![]() ,
,![]() ,先将
,先将![]() 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到![]() .
.

(1)在图中画出![]() ;
;
(2)点![]() ,
,![]() 的坐标分别为______、______;
的坐标分别为______、______;
(3)若![]() 轴有一点
轴有一点![]() ,使
,使![]() 与
与![]() 面积相等,求出
面积相等,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,在平面直角坐标系xOy中,将抛物线![]() 的对称轴绕着点P(
的对称轴绕着点P(![]() ,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
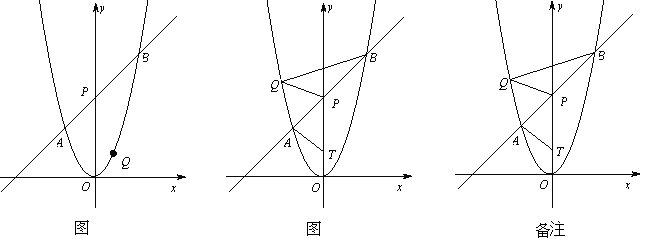
(1)求直线AB的函数表达式;
(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;
(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是直线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两边平方和等于第三边平方的两倍的三角形叫做“奇异三角形”.
(1)根据“奇异三角形”的定义,请你判断命题:“等边三角形一定是奇异三角形” 是 命题.(填写“真命题、假命题”)
(2)在RtΔABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若RtΔABC是“奇异三角形”,则a:b:c= .
(3)如图,在四边形ACBD中,∠ACB=∠ADB=90°,AD=BD,若在四边形ACBD内存在点E使得AE=AD,CB=CE.
①求证:ΔACE是“奇异三角形”;
②当ΔACE是直角三角形时,且AC=![]() ,求线段AB 的长.
,求线段AB 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图(2)形状拼成一个正方形.
①图(2)中的空白部分的边长是多少?(用含a,b的式子表示)
②观察图(2),用等式表示出![]() ,ab和
,ab和![]() 的数量关系;
的数量关系;

(2)如图所示,在△ABC与△DCB中,AC与BD相交于点E,且∠A=∠D,AB=DC.求证:△ABE≌△DCE;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,还需再添加两个条件才能使
,还需再添加两个条件才能使![]() ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如右表所示:图二是某同学根据上表绘制的一个不完整的条形图.请你根据以上信息解答下列问题:
(1)补全图一和图二.
(2)请计算每名候选人的得票数.
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com