
【题目】(1)如图(1),将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图(2)形状拼成一个正方形.
①图(2)中的空白部分的边长是多少?(用含a,b的式子表示)
②观察图(2),用等式表示出![]() ,ab和
,ab和![]() 的数量关系;
的数量关系;

(2)如图所示,在△ABC与△DCB中,AC与BD相交于点E,且∠A=∠D,AB=DC.求证:△ABE≌△DCE;

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(0,3),B点的坐标为(-3.0),D为x轴上的一个动点,AE⊥AD,且AE=AD,连接BE交y轴于点M
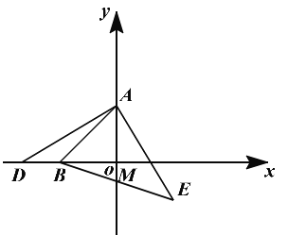
(1)若D点的坐标为(-5.0),求E点的坐标:
(2)求证:M为BE的中点
(3)当D点在x轴上运动时,探索:![]() 为定值
为定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为____.
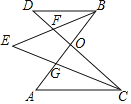
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若|x+2y-10|+|2x-y|=0,试分别求出1秒钟后△AOB的面积;
(2)如图2,所示,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图3所示,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,设∠AGH=α,∠BGC=β,试探究出α和β满足的数量关系并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.

(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年年初,新型冠状病毒在武汉等地区肆虐,为了缓解湖北地区的疫情,全国各地的医疗队员都纷纷报名支援湖北,某方舱医院需要8组医护人员支援,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人,若每组人数比预定人数少分配一人,则总数不够90人,那么预定每组分配的人数是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安庆市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益,2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(每亩产出-每亩投入=每亩纯收入)
种类 | 投入(元) | 产出(元) |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?
(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com