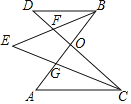
[题目]如图所示.AB.CD相交于点O.若BE平分∠ABD交CD于F.CE平分∠ACD交AB于G.∠A=45°.∠BEC=40°.则∠D的度数为．题目和参考答案——青夏教育精英家教网—

【题目】如图所示，AB、CD相交于点O，若BE平分∠ABD交CD于F，CE平分∠ACD交AB于G，∠A=45°，∠BEC=40°，则∠D的度数为____．

【答案】35°．

【解析】

先根据角平分线定义得到∠1=∠2，∠3=∠4，再利用三角形内角和定理和对顶角相等得到∠1+∠D=∠4+∠E①，∠1+∠2+∠D=∠3+∠4+∠A，即2∠1+∠D=2∠4+∠A②，接着利用①×2-②得2∠E=（∠D+∠A），由此即可解决问题．

如图，

∵BE平分∠DBA交DC于F，CE平分∠DCA交AB于G，

∴∠1=∠2，∠3=∠4，

∵∠1+∠D=∠4+∠E①，

∠1+∠2+∠D=∠3+∠4+∠A，即2∠1+∠D=2∠4+∠A②，

由①×2-②得∠D=2∠E-∠A，

∵∠A=45°，∠BEC=40°，

∴∠D=35°，

故答案为35°．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】水利部门为加强防汛工作，决定对某水库大坝进行加固，大坝的横截面是梯形ABCD，如图所示，已知迎水坡面AB的长为16米，∠B＝60°，背水坡面CD的长为16米，加固后大坝的横截面为梯形ABED，CE的长为8米．

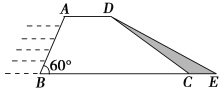
(1)已知需加固的大坝长为150米，求需要填土石方多少立方米？

(2)求加固后的大坝背水坡面DE的坡度．

查看答案和解析>>

科目：初中数学 来源： 题型：

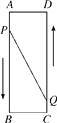
【题目】如图，已知A，B，C，D为矩形的四个顶点，AB＝16 cm，AD＝6 cm，动点P，Q分别从点A，C同时出发，点P以3 cm/s的速度向点B移动，一直到点B为止，点Q以2 cm/s的速度向点D移动，当点P停止运动时，点Q也停止运动．问：

(1)P，Q两点从开始出发多长时间时，四边形PBCQ的面积是33 cm2?

(2)P，Q两点从开始出发多长时间时，点P与点Q之间的距离是10 cm?

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】综合与探究

如图是一个正方形纸片，如果将正方形纸片绕点逆时针旋转角度，得到正方形，交于点，的延长线交于点，连接、．

（1）求证：平分；

（2）直接写出线段、、之间的数量关系；

（3）连接，，，，试探究在旋转过程中，四边形能否成为矩形？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读以下材料，并按要求完成相应的任务．

课题学习:如何解一元二次不等式？

例题:解一元二次不等式．

解：

．

由有理数的乘法法则“两数相乘，同号得正”，有：

解不等式组得:

的解集为或．

即:一元二次不等式的解集为或．

任务：（1）上面解一元二次不等式的过程中体现出了数学的一些基本思想方法，请在下列选项中选出你认为正确的一项：_____ ；(填选项即可)

A.分类讨论思想；B.数形结合思想；C.公理化思想；D.函数思想

（2）求一元二次不等式的解集为：_____ ；(直接填写结果，不写解答过程)

（3）仿照例题中的数学思想方法，求分式不等式的解集．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（本题满分12分）如图，在平面直角坐标系xOy中，将抛物线的对称轴绕着点P（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.

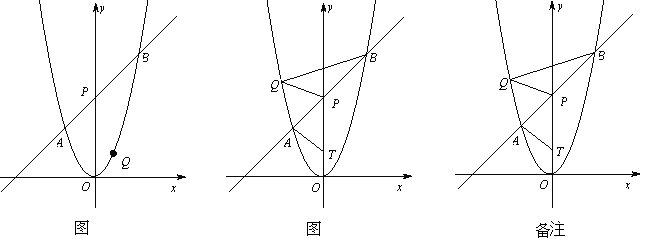
（1）求直线AB的函数表达式；

（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；

（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.

查看答案和解析>>

科目：初中数学 来源： 题型：

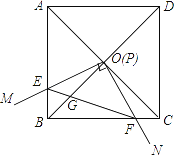
【题目】如图，边长为1的正方形ABCD的对角线AC、BD相交于点O，有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是________．

（1）EF=OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）BE+BF= OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=．