
����Ŀ���������ھ���ƶ��У��������ָ��ũ�������ֲ�ṹ��������ֲЧ�棬2018������ڹ����ӵİ����£��ƻ���ֲ���������߲˹�15Ķ��Ԥ��ÿĶ��Ͷ����������±�����ÿĶ����-ÿĶͶ��=ÿĶ�����룩
���� | Ͷ�루Ԫ�� | ������Ԫ�� |
������ | 1000 | 4500 |
�߲� | 1200 | 5300 |
��1�������15Ķ�صĴ�����Ҫ�ﵽ54900Ԫ������ֲ���������߲˸�����Ķ��
��2�������Ͷ�벻����16000Ԫ���������ֲ�߲˶���Ķ���������15Ķ�صĴ������Ƕ��٣�
���𰸡���1������ֲ������11Ķ������ֲ�߲�4Ķ����2�������ֲ�߲�5Ķ���������15Ķ�صĴ�������55500Ԫ.
��������
��1��������ֲ������xĶ������ֲ�߲�yĶ�����ݵ�����ϵ��һ��15Ķ�أ���15Ķ�صĴ�����Ҫ�ﵽ54900Ԫ���г�����x��y�Ķ�Ԫһ�η����飬������ɣ�
��2������ֲ������aĶ��������ֲ�߲ˣ�15-a��Ķ����������Ͷ�벻����16000Ԫ�����г�����a��һԪһ�β���ʽ��������ɣ�
��1��������ֲ������![]() Ķ������ֲ�߲�
Ķ������ֲ�߲�![]() Ķ����������
Ķ����������
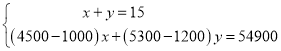 ��
��
���![]() .
.
������ֲ������11Ķ������ֲ�߲�4Ķ��
��2������ֲ������![]() Ķ��������ֲ�߲�
Ķ��������ֲ�߲�![]() Ķ����������
Ķ����������
![]() ��
��
���![]() ��
��
![]() ��Ķ����
��Ķ����
![]()
![]()
![]() ��Ԫ��.
��Ԫ��.
�������ֲ�߲�5Ķ���������15Ķ�صĴ�������55500Ԫ.


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У���A��BΪ����Lͼ���ϵ��������㣬��A����Ϊ��x1 �� y1������B����Ϊ��x2 �� y2������ʽ�� ![]() ��Ϊ����L��x1��x2��ƽ���仯�ʣ����ں���K��y=2x2��3x+1ͼ����������A��x1 �� y1����B��x2 �� y2������x1=1��x2��x1=
��Ϊ����L��x1��x2��ƽ���仯�ʣ����ں���K��y=2x2��3x+1ͼ����������A��x1 �� y1����B��x2 �� y2������x1=1��x2��x1= ![]() ʱ������K��x1��x2��ƽ���仯��������x1=1��x2��x1=
ʱ������K��x1��x2��ƽ���仯��������x1=1��x2��x1= ![]() ��nΪ��������ʱ������K��x1��x2��ƽ���仯���� ��
��nΪ��������ʱ������K��x1��x2��ƽ���仯���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�б�ʾһ�κ��� y mx n ������������ y nx��m �� n �dz������� mn 0�� ͼ����ǣ� ��
A. B.
B. C.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ĸ�ѧ����ѧϰģʽ���䡰��ʦҪѧ��ѧϰ��Ϊ��ѧ������ѧϰ����������ѧ������ѧϰ���������������л��ͬѧ�͡�����ϲ������ѧϰ��ʽ�����������������Χ��һЩͬѧ�������ռ��������ݻ���������������������ͳ��ͼ����ͼ����

���������������������ͳ��ͼ�ش�����4�����⣺
��1����γ��������У���������������ѧ����
��2����ȫ����ͳ��ͼ�е�ȱ�
��3��������ͳ��ͼ�У�ѡ���ʦ���ڵ���ռԲ�ĽǵĶ���Ϊ������
��4�����ݵ������������У1800��ѧ���д�Լ�ж�����ѡ��С�����ѧϰģʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
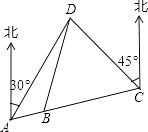
����Ŀ��ij�п�չһ�����г����λ����·�辭A��B��C��D�ĵأ���ͼ������A��B��C������ͬһֱ���ϣ�D����A�ر�ƫ��30�㷽����C�ر�ƫ��45�㷽��C����A�ر�ƫ��75�㷽����BC=CD=20km������������·��A�ص�D�ص�·�̴�Լ�Ƕ��٣�������������������ο����ݣ�sin15���0.25��cos15���0.97��tan15���0.27�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90������C��50����AH��BD�ֱ��ǡ�ABC�ߺͽ�ƽ���ߣ���PΪ��BC��һ���㣬����BDPΪֱ��������ʱ�����CDP��_____�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=90�㣬AB=AC��DΪBC���е㣮
��1����ͼ1��д����D����ABC��������A��B��C�ľ���Ĺ�ϵ��ֱ��д�����ۣ���
��2����ͼ1����E��F�ֱ���AB��AC�ϵĵ㣬��BE=AF����֤����DEF�ǵ���ֱ�������Σ�
��3������E��F�ֱ���AB��CA���ӳ����ϵĵ㣬����BE=AF�������������䣬���жϡ�DEF����״����ֱ��д���ۣ���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������ʣ����ڵ����������У��ȱ߶ԵȽ�����������ͼ1���ڡ�ABC�У���AB=AC�����B=��C�����ô����ʽ���������⣺
��ͼ2�����ı���ABCD�У�AD��BC����E�ڱ�AD�ϣ���CB=CE����F������ED�ϵ�һ�����㣬��ECF��ƽ����CG��BE���ӳ����ڵ�G��
��1������EBC=68������ECF=40������G�Ķ�����
��2���ڶ���F�˶��Ĺ����У���G����EFC��ֵ�Ƿ����仯�������䣬������ֵ�����仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y��z��15����3x��y��z����25��x��y��z��Ϊ�Ǹ���������ʽ5x+4y+z�����ֵΪa����СֵΪb����a��b =________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com