
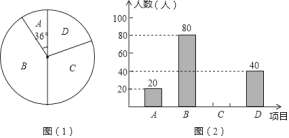
【题目】计划开设以下课外活动项目:A 一版画、B 一机器人、C 一航模、D 一园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生 必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;扇形统计图中,选“D一园艺种植”的学生人数所占圆心角的度数是 °;
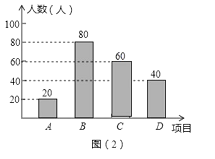
(2)请你将条形统计图补充完整;
(3)若该校学生总数为 1500 人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总 人数
【答案】(1)200;72(2)60(人),图见解析(3)1050人.
【解析】
(1)由A类有20人,所占扇形的圆心角为36°,即可求得这次被调查的学生数,再用360°乘以D人数占总人数的比例可得;
(2)首先求得C项目对应人数,即可补全统计图;
(3)总人数乘以样本中B、C人数所占比例可得.
(1)∵A类有20人,所占扇形的圆心角为36°,
∴这次被调查的学生共有:20÷![]() =200(人);
=200(人);
选“D一园艺种植”的学生人数所占圆心角的度数是360°×![]() =72°,
=72°,
故答案为:200、72;
(2)C项目对应人数为:200208040=60(人);
补充如图.
(3)1500×![]() =1050(人),
=1050(人),
答:估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数为1050人.


科目:初中数学 来源: 题型:
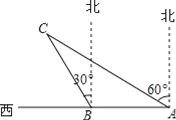
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
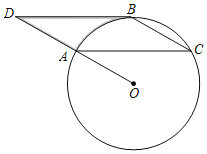
【题目】如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)图中线段AD、BD和![]() 围成的阴影部分的面积= .
围成的阴影部分的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3AB=3![]() ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.
,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
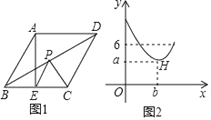
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
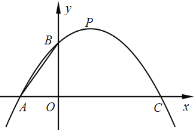
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
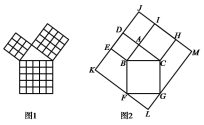
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
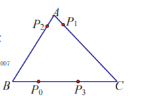
【题目】电子跳蚤游戏盘是如图所示的![]() ,
,![]() .如果跳蚤开始时在
.如果跳蚤开始时在![]() 边的
边的![]() 处,
处,![]() .跳蚤第一步从
.跳蚤第一步从![]() 跳到
跳到![]() 边的
边的![]() (第1次落点)处,且
(第1次落点)处,且![]() ;第二步从
;第二步从![]() 跳到
跳到![]() 边的
边的![]() (第2次落点)处,且
(第2次落点)处,且![]() ;第三步从
;第三步从![]() 跳到
跳到![]() 边的
边的![]() (第3次落点)处,且
(第3次落点)处,且![]() ;……;跳蚤按上述规则一直跳下去,第
;……;跳蚤按上述规则一直跳下去,第![]() 次落点为
次落点为![]() (
(![]() 为正整数),则点
为正整数),则点![]() 与
与![]() 之间的距离为( )
之间的距离为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com