
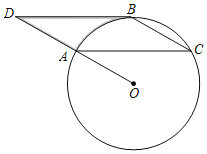
【题目】如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)图中线段AD、BD和![]() 围成的阴影部分的面积= .
围成的阴影部分的面积= .
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OB,交CA于E,,根据圆周角定理求出∠BOA=60°,根据∠BCA=∠OAC=30°和三角形内角和定理求出∠AEO=90°,即OB⊥AC,根据BD∥AC,得到∠DBE=∠AEO=90°,可得BD是⊙O的切线;
(2)根据平行线的性质得到∠D=30°,解直角三角形求出BD,分别求出△BOD的面积和扇形AOB的面积,即可得出答案.
(1)证明:如图示,连接OB,交CA于E,
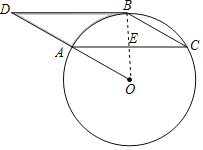
∵∠C=30°,∠C=![]() ∠BOA,
∠BOA,
∴∠BOA=60°,
∵∠BCA=∠OAC=30°,
∴∠AEO=90°,
即OB⊥AC,
∵BD∥AC,
∴∠DBE=∠AEO=90°,
∴BD是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,
∴∠D=∠CAO=30°,
∵∠OBD=90°,OB=8,
∴BD=![]() OB=8
OB=8![]() ,
,
∴S阴影=S△BDO﹣S扇形AOB=![]() ×8×8
×8×8![]() ﹣
﹣![]() =32
=32![]() ﹣
﹣![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.732,tan20°≈0.36,结果精确到0.1)
≈1.732,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为圆外一点,AC交⊙O于点D,BC2=CDCA,弦ED=弦BD,BE交AC于F.

(1)求证:BC为⊙O切线;
(2)判断△BCF的形状并说明理由;
(3)已知BC=15,CD=9,求tan∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
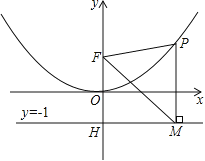
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,初三数学兴趣小组同学为了测量垂直于水平地面的一座大厦AB的高度,一测量人员在大厦附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了60米后到达D处,在D处测得A处的仰角大小为30°,则大厦AB的高度约为多少米?(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
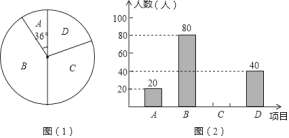
【题目】计划开设以下课外活动项目:A 一版画、B 一机器人、C 一航模、D 一园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生 必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;扇形统计图中,选“D一园艺种植”的学生人数所占圆心角的度数是 °;
(2)请你将条形统计图补充完整;
(3)若该校学生总数为 1500 人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总 人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正三角形的网格中,
的正三角形的网格中,![]() 的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
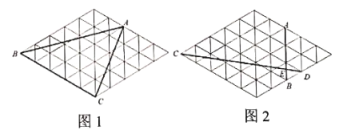
(1)在图1中,画出![]() 的
的![]() 边上的中线
边上的中线![]() .
.
(2)在图2中,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com