
【题目】如图,AB为⊙O的直径,C为圆外一点,AC交⊙O于点D,BC2=CDCA,弦ED=弦BD,BE交AC于F.

(1)求证:BC为⊙O切线;
(2)判断△BCF的形状并说明理由;
(3)已知BC=15,CD=9,求tan∠ADE的值.
【答案】(1)证明见解析;(2)△BCF为等腰三角形.证明见解析;(3)![]()
【解析】
(1)由BC2=CDCA,根据三角形相似的判定得到△CBD∽△CAB,根据三角形相似的性质得到∠CBD=∠BAC,而AB为⊙O的直径,根据圆周角定理的推论得∠ADB=90°,易证得∠ABD+∠CBD=90°,根据切线的判定即可得到答案;
(2)由![]() ,根据圆周角定理得∠DAE=∠BAC,由(1)得∠BAC=∠CBD,则∠CBD=∠DAE,根据同弧所对的圆周角相等得∠DAE=∠DBF,所以∠DBF=∠CBD,而∠BDF=90°,根据等腰三角形三线的判定即可得到△BCF为等腰三角形;
,根据圆周角定理得∠DAE=∠BAC,由(1)得∠BAC=∠CBD,则∠CBD=∠DAE,根据同弧所对的圆周角相等得∠DAE=∠DBF,所以∠DBF=∠CBD,而∠BDF=90°,根据等腰三角形三线的判定即可得到△BCF为等腰三角形;
(3)由BC2=CDCA,BC=15,CD=9,可计算出CA=25,根据等腰三角形的性质有BF=BC=15,DF=DC=9,利用勾股定理计算出BD=12,得到AF=7,再根据等积可求出AE=![]() ,然后利用Rt△AEF∽Rt△BDF,通过相似比可计算出EF,则可得到BE,而∠ADE=∠ABE,最后利用三角函数的性质可计算出tan∠ADE的值.
,然后利用Rt△AEF∽Rt△BDF,通过相似比可计算出EF,则可得到BE,而∠ADE=∠ABE,最后利用三角函数的性质可计算出tan∠ADE的值.
(1)证明:∵BC2=CDCA,
∴BC:CA=CD:BC,
∵∠C=∠C,
∴△CBD∽△CAB,
∴∠CBD=∠BAC,
又∵AB为⊙O的直径,
∴∠ADB=90°,即∠BAC+∠ABD=90°,
∴∠ABD+∠CBD=90°,即AB⊥BC,
∴BC为⊙O切线;
(2)△BCF为等腰三角形.证明如下:
∵![]() ,
,
∴∠DAE=∠BAC,
又∵△CBD∽△CAB,
∴∠BAC=∠CBD,
∴∠CBD=∠DAE,
∵∠DAE=∠DBF,
∴∠DBF=∠CBD,
∵∠BDF=90°,
∴∠DBC=∠BDF=90°
∵BD=BD
∴△BDF≌△BDC
∴BF=BC
∴△BCF为等腰三角形;
(3)解:∵BC2=CDCA,BC=15,CD=9,
∴CA=25,BF=BC=15,DF=DC=9,
∴BD=![]() =12,
=12,
∴AF=25-18=7,
∴S△ABF=![]() AEBF=
AEBF=![]() AFBD,
AFBD,
∴AE=![]() ,
,
易证Rt△AEF∽Rt△BDF,
∴EF:DF=AF:BF,即EF:9=7:15,
∴EF=![]() ,
,
∴BE=15+![]() =
=![]() ,
,
∵∠ADE=∠ABE,
∴tan∠ADE=tan∠ABE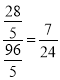 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于任意一个四位数,我们可以记为![]() ,即
,即![]() .若规定: 对四位正整数
.若规定: 对四位正整数![]() 进行 F运算,得到整数
进行 F运算,得到整数![]() .例如,
.例如,![]() ;
;![]() .
.
(1)计算:![]() ;
;
(2)当![]() 时,证明:
时,证明:![]() 的结果一定是4的倍数;
的结果一定是4的倍数;
(3)求出满足![]() 的所有四位数.
的所有四位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
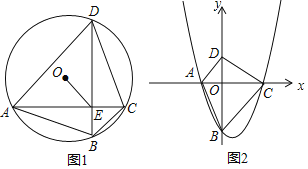
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “十字形”.(填“是”或“不是”)
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;
①![]() =
=![]()
![]() ;②
;②![]()
![]() =
=![]()
![]() ;③“十字形”ABCD的周长为12
;③“十字形”ABCD的周长为12![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
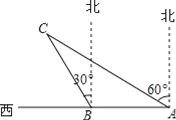
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
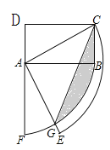
【题目】如图,矩形ABCD中,AD=1,CD=![]() ,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为__.
,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
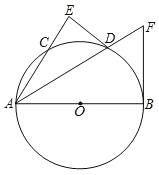
【题目】如图,AB是直经,D是![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
(1)求证:DE是⊙O的切线.
(2)试探究AE,AD,AB三者之间的等量关系.
(3)若DE=3,⊙O的半径为5,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
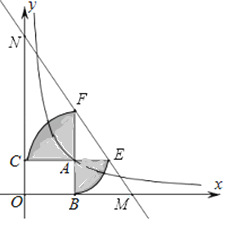
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
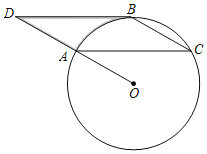
【题目】如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)图中线段AD、BD和![]() 围成的阴影部分的面积= .
围成的阴影部分的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
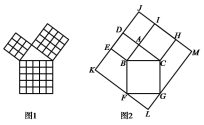
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com