
【题目】如图,在![]() 的正三角形的网格中,
的正三角形的网格中,![]() 的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
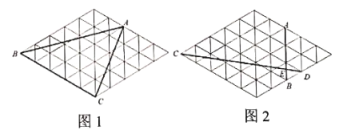
(1)在图1中,画出![]() 的
的![]() 边上的中线
边上的中线![]() .
.
(2)在图2中,求![]() 的值.
的值.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)利用平行四边形的性质分别作出AB、AC的中点E、F,再利用三角形重心的性质即可作出△ABC的BC边上的中线AD;
(2)利用平行线的性质可得∠AEC=∠FDC,再利用菱形及等边三角形的性质可求得DH、CH的长,继而求得CD的长,从而求得答案.
(1)如图,线段AD就是所求作的中线;
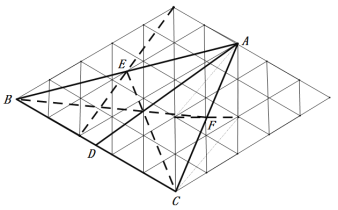
(2)如图:在![]() 的正三角形的网格中,
的正三角形的网格中,
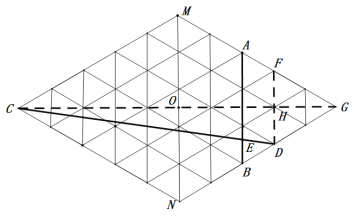
∵MN∥AB∥FD,
∴∠AEC=∠FDC,
∵四边形CMGN为菱形,且边长为5,
∴CG⊥MN,
∴CG⊥FD,
![]() ,
,
∴CG=2OG=5![]() ,
,
∵△GFD为等边三角形,且边长为2,
同理:HG=![]() ,
,
∴在Rt△CDH中,∠CHD=90![]() ,DH=1,CH=CG-HG=4
,DH=1,CH=CG-HG=4![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
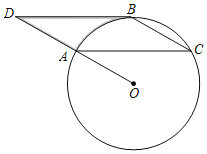
【题目】如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)图中线段AD、BD和![]() 围成的阴影部分的面积= .
围成的阴影部分的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
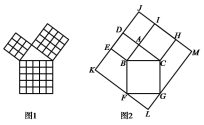
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
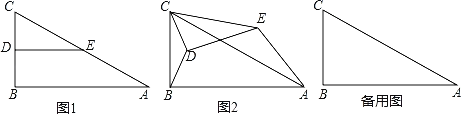
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
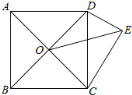
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
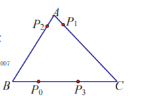
【题目】电子跳蚤游戏盘是如图所示的![]() ,
,![]() .如果跳蚤开始时在
.如果跳蚤开始时在![]() 边的
边的![]() 处,
处,![]() .跳蚤第一步从
.跳蚤第一步从![]() 跳到
跳到![]() 边的
边的![]() (第1次落点)处,且
(第1次落点)处,且![]() ;第二步从
;第二步从![]() 跳到
跳到![]() 边的
边的![]() (第2次落点)处,且
(第2次落点)处,且![]() ;第三步从
;第三步从![]() 跳到
跳到![]() 边的
边的![]() (第3次落点)处,且
(第3次落点)处,且![]() ;……;跳蚤按上述规则一直跳下去,第
;……;跳蚤按上述规则一直跳下去,第![]() 次落点为
次落点为![]() (
(![]() 为正整数),则点
为正整数),则点![]() 与
与![]() 之间的距离为( )
之间的距离为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )

A.∠A=60°B.△ACD是直角三角形
C.BC=![]() CDD.点B是△ACD的外心
CDD.点B是△ACD的外心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com