
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一动点(
上一动点(![]() 不与
不与![]() ,
,![]() 重合).
重合).
(1)如图1,当点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
(2)连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于点
于点![]() .若
.若![]() 时,如图2.
时,如图2.
①![]() ______;
______;
②求证:![]() 为等腰三角形;
为等腰三角形;
(3)连接CD,∠CDE=30°,在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请求出
的形状可以是等腰三角形吗?若可以,请求出![]() 的度数;若不可以,请说明理由.
的度数;若不可以,请说明理由.

【答案】(1)证明见解析;(2)①120°;②证明见解析;(3)![]() 可以是等腰三角形,此时
可以是等腰三角形,此时![]() 的度数为
的度数为![]() 或
或![]() .
.
【解析】
(1)先证明△ACD与△BFD全等,即可得出结论;
(2)①先根据等边对等角及三角形的内角和求出∠B的度数,再由平行线的性质可得出∠ADE的度数,最后根据平角的定义可求出∠CDB的度数;②根据等腰三角形的性质以及平行线的性质可得出∠A=∠EDA,从而可得出结论;
(3)先假设△ECD可以是等腰三角形,再分以下三种情况:I.当![]() 时,
时,![]() ;II.当
;II.当![]() 时,
时,![]() ;III.当
;III.当![]() 时,
时,![]() ,然后再根据等腰三角形的性质、三角形的内角和以及三角形外角的性质求解即可.
,然后再根据等腰三角形的性质、三角形的内角和以及三角形外角的性质求解即可.
(1)证明:![]() ,
,![]() 是
是![]() 的中线,
的中线,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ;
;
(2)①解:∵AC=BC,∠ACB=120°,
∴∠A=∠B=(180°-120°)÷2=30°,
又DE∥BC,
∴∠ADE=∠B=30°,
∴∠CDB=180°-∠ADE-∠EDC=120°,
故答案为:![]() ;
;
②证明:![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() 为等腰三角形.
为等腰三角形.
(3)解:![]() 可以是等腰三角形,理由如下:
可以是等腰三角形,理由如下:
I.当![]() 时,
时,![]() ,如图3,
,如图3,
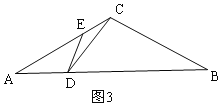
![]() .
.
![]() ,
,
![]() .
.
II.当![]() 时,
时,![]() ,如图4,
,如图4,
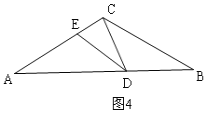
![]() ,
,
![]() .
.
![]() .
.
III.当![]() 时,
时,![]() .
.
∴![]() ,
,
![]() ,
,
![]() 此时,点
此时,点![]() 与点
与点![]() 重合,不合题意.
重合,不合题意.
综上所述,![]() 可以是等腰三角形,此时
可以是等腰三角形,此时![]() 的度数为
的度数为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
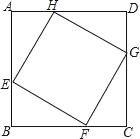
【题目】如图,在正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边上的动点,且AE=BF=CG=DH.
(1)求证:△AEH≌△CGF;
(2)在点E、F、G、H运动过程中,判断直线EG是否经过某一个定点,如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
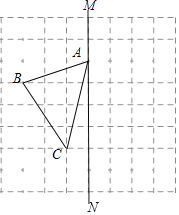
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
(1)△ABC的面积为 ;
(2)在图中作出△ABC关于直线MN的对称图形△A'B'C';
(3)在MN上找一点P,使得PB+PC的距离最短,这个最短距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图1,已知锐角△ABC中,点D在BC边上,当线段AD最短时,请你在图中画出点D的位置.
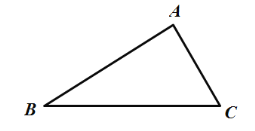
图1
(2)若一个四边形的四个顶点分别在一个三角形的三条边上;则称这个四边形为该三角形的内接四边形.
如图2,在Rt△ABC中,AB=6,BC=8,∠B=90°.矩形BEFG是△ABC的内接矩形,若EF=2,则矩形BEFG的面积为_________
如图3,在△ABC中,AB=![]() ,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
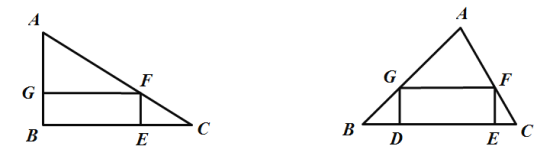
图2 图3
问题解决:
(3)如图4,△ABC是一块三角形木板余料,AB=6,BC=8,∠B=30°,木匠师傅想利用它裁下一块矩形DEFG木块,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上,请在图4中画出对角线DF最短的矩形DEFG,请说明理由,并求出此时DF的长度.
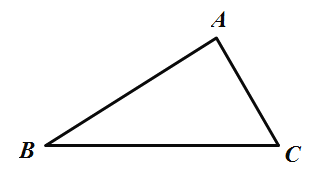
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
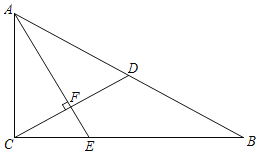
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,已知∠BAD=120°,∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于E、F.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
(1)如图甲,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:
①如图乙,当顶点G运动到AC的中点时,请直接写出线段EC、CF与BC的数量关系(不需要写出证明过程);
②如图丙,在顶点G运动的过程中,若![]() ,探究线段EC、CF与BC的数量关系;
,探究线段EC、CF与BC的数量关系;
(3)问题解决:如图丙,已知菱形的边长为8,BG=7,CF=![]() ,当
,当![]() >2时,求EC的长度。
>2时,求EC的长度。
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)求出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式,S是否有最大值?如有,请求出最大值,没有请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
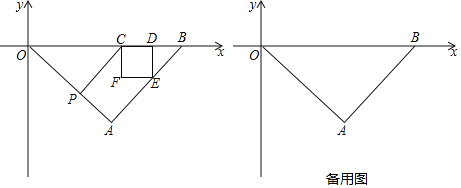
【题目】如图,平面直角坐标系中,点A在第四象限,点B在x轴正半轴上,在△OAB中,∠OAB=90°,AB=AO=6![]() ,点P为线段OA上一动点(点P不与点A和点O重合),过点P作OA的垂线交x轴于点C,以点C为正方形的一个顶点作正方形CDEF,使得点D在线段CB上,点E在线段AB上.
,点P为线段OA上一动点(点P不与点A和点O重合),过点P作OA的垂线交x轴于点C,以点C为正方形的一个顶点作正方形CDEF,使得点D在线段CB上,点E在线段AB上.
(1)①求直线AB的函数表达式.
②直接写出直线AO的函数表达式 ;
(2)连接PF,在Rt△CPF中,∠CFP=90°时,请直接写出点P的坐标为 ;
(3)在(2)的前提下,直线DP交y轴于点H,交CF于点K,在直线OA上存在点Q.使得△OHQ的面积与△PKE的面积相等,请直接写出点Q的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com