
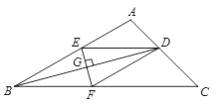
【题目】如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.
(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长.
【答案】(1)证明见解析;
(2)CF的长为2+![]()
【解析】试题分析:(1)本题利用垂直平分线的性质,角平分线的性质得出结论,证明四边形BFDE为菱形即可;(2)本题要根据菱形得出三角形DFC的角的度数,作垂直构造特殊的三角形解决问题即可.
试题解析:(1)证明:∵EF垂直平分BD,
∴EB=ED,FB=FD.
∵BD平分∠ABC交AC于D,
∴∠ABD=∠CBD.
∵∠ABD+∠BEG=90°,∠CBD+∠BFG=90°,
∴∠BEG=∠BFG.
∴BE=BF.
∴四边形BFDE是菱形.
∴DE=DF.
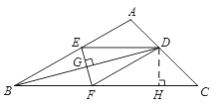
(2)解:过D作DH⊥CF于H.
∵四边形BFDE是菱形,
∴DF∥AB,DE=DF=4.
在Rt△DFH中,∠DFC=∠ABC=30°,
∴DH=2.
∴FH=![]() .
.
在Rt△CDH中,∠C=45°,
∴DH=HC=2.
∴CF=2+![]() .
.


科目:初中数学 来源: 题型:
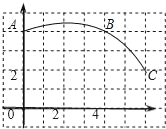
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
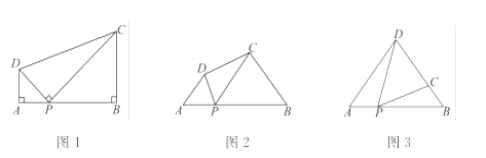
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() 米,
米,![]() 米,
米,![]() 点位于
点位于![]() 点的南偏西
点的南偏西![]() 方向,
方向,![]() 点位于
点位于![]() 点的南偏东
点的南偏东![]() 方向.
方向.
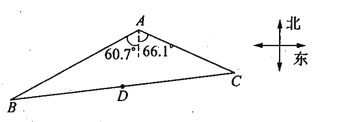
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0.1米)
间的距离.(结果精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=2x+2m(m>0)与x,y轴分别交于A.B两点,点M是双曲线![]() (x>0)上一点,分别连接MA、MB.
(x>0)上一点,分别连接MA、MB.
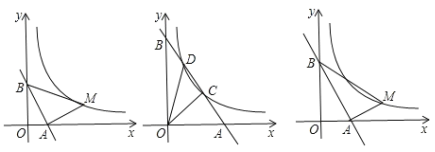
(1)如图,当点A(![]() ,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
(2)如图,当m=3时,直线l与双曲线交于C.D两点,分别连接OC、OD,试求△OCD面积;
(3)如图,在双曲线上是否存在点M,使得以AB为直角边的△MAB与△AOB相似?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,画一条平行于BC的直线,使其将△ABC分成两部分,且所分三角形与梯形面积比为1:3;
(2)如图②,△ABC中AB=4,AC=3,BC=6,D是△ABC中AC边上的点,AD=2,过点D画一条直线l将△ABC分成两部分,l与△ABC另一边的交点为点P,使其所分的一个三角形与△ABC相似,并求出DP的长;
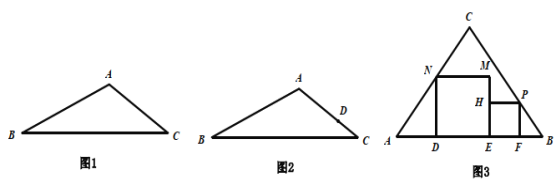
(3)如图③所示,在等腰△ABC中,CA=CB=10,AB=12.在△ABC中放入正方形DEMN和正方形EFPH,使得DE.EF在边AB上,点P.N分别在边CB.CA上,若较大正方形的边长为a,请用含a的代数式表示较小正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=" 3" cm,BC=" 4" cm.点P从点A出发,以1 cm/s的速度沿AB运动;同时,点Q从点B出发,以2 cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
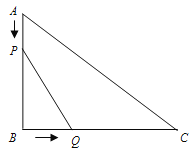
(1)试写出△PBQ的面积 S (cm2)与动点运动时间 t (s)之间的函数表达式;
(2)运动时间 t 为何值时,△PBQ的面积最大?最大值是多少?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com