
����Ŀ��ֱ��l��y=2x+2m(m>0)��x��y��ֱ���A.B���㣬��M��˫����![]() (x>0)��һ�㣬�ֱ�����MA��MB.
(x>0)��һ�㣬�ֱ�����MA��MB.
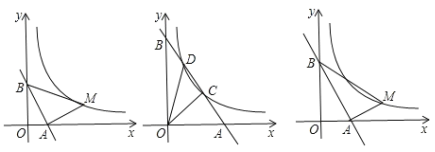
(1)��ͼ������A(![]() ��0)ʱ��ǡ��AB=AM����MAB=90��������M�����ꣻ
��0)ʱ��ǡ��AB=AM����MAB=90��������M�����ꣻ
(2)��ͼ����m=3ʱ��ֱ��l��˫���߽���C.D���㣬�ֱ�����OC��OD��������OCD�����
(3)��ͼ����˫�������Ƿ���ڵ�M��ʹ����ABΪֱ�DZߵ���MAB����AOB����?������ڣ���ֱ��д����M�����ꣻ��������ڣ���˵������.
���𰸡���1����![]() ��
��![]() ������2��3����3����4��1������2��2������
������2��3����3����4��1������2��2������![]() ��
��![]() ������
������![]() ��
��![]() ��.
��.
��������
��1����A���������ֱ�ߵĽ���ʽ�������m��ֵ��Ȼ��֤����OAB�ա�EMA�����ME��AE�ij�����M�����꼴����⣻
��2����һ�κ����뷴���������Ľ���ʽ��ɵķ����飬�������C��D�����꣬��DF��y���ڵ�F��CG��y�ᣬ����S��OCD=S����CDFG+S��OCG-S��ODF��⣻
��3���������ۣ��ԡ�BAM�͡�ABMΪֱ������������ٵ���BAM=��BOA=90��ʱ����MH��x���ڵ�H�������AM�ij����ٸ������������ε��������AH��MH�ij����������M�����꣬���뷴����������ϵʽ���m���ɣ��ڵ���ABM=90��ʱ������M��MH��y���ڵ�H��ͬ�������M����.
(1)��A(![]() ��0)����y=2x+2m�ã�
��0)����y=2x+2m�ã�![]() +2m=0��
+2m=0��
��ã�m=![]() .
.
��ֱ�ߵĽ���ʽ�ǣ�y=2x+![]() ��
��
��x=0,���y=![]() ��
��
��B��������(0, ![]() ).
).
��ͼ��ʾ����ME��x���ڵ�E.
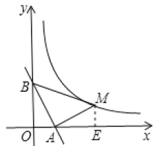
�ߡ�BAM=90�㣬
���BAO+��MAE=90�㣬
�֡�ֱ�ǡ�AEM��,��AME+��MAE=90�㣬
���BAO=��AME.
�ڡ�OAB�͡�EMA�У�
���OAB�ա�EMA(AAS)��
��ME=OA=![]() ,AE=OB=
,AE=OB=![]() .
.
��OE=OA+AE=![]() ��
��
��M��������(![]() ��
��![]() )��
)��
(2)��m=3ʱ��һ�κ����Ľ���ʽ��y=2x+6.
�ⲻ��ʽ��![]() ��
��
��![]() ��
��![]() ��
��
��D��������(1,4),C��������(2,2).
��ͼ����DF��y���ڵ�F��CG��y��,��F��G������ֱ���(0,4)��(0,2).
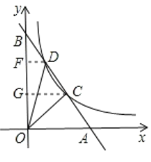
��S��OCG=S��ODF=![]() ��4=2��
��4=2��
S����CDFG=![]() ��(1+2)��(42)=3��
��(1+2)��(42)=3��
��S��OCD=S����CDFG+S��OCGS��ODF=3;
(3)��ͼ����MH��x���ڵ�H.
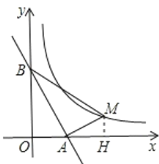
���AOB����ABM����AMH������ֱ�DZߵı���1:2��ֱ��������.
�ٵ���BAM=��BOA=90��ʱ��OA=m��OB=2m���ã�
AM=![]() AB=
AB=![]() m��MH=
m��MH=![]() OA=
OA=![]() ��
��
�Ӷ��õ���M������Ϊ(2m, ![]() ).
).
����˫���߽���ʽΪ��![]() =
=![]() ��
��
��ã�m=2,���M������Ϊ(4,1)��
ͬ������BAM=��OBAʱ,����õ�M������Ϊ(![]() ��
��![]() ).
).
�ڵ���ABM=90��ʱ������M��MH��y���ڵ�H��
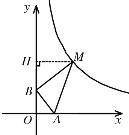
���AOB����ABM����BMH����ֱ�DZߵı���1:2��ֱ�������Σ�
����AMB=��OABʱ��OB=m��OA=2m��
�ã�AH=2OB=2m��MH=2OA=4m��
�Ӷ���M������Ϊ(4m,4m)
����˫���ߵĽ���ʽ�ã�4m��4m=4��
��ã�m=![]() ,��M������Ϊ(2,2)��
,��M������Ϊ(2,2)��
ͬ��,����AMB=��OBAʱ,��M������Ϊ(![]() ,
,![]() ).
).
�������������������ĵ�M�������ǣ���4��1������2��2������![]() ��
��![]() ������
������![]() ��
��![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=cx2��2cx��3c��c��0����������˵������ȷ���ǣ��������� ��
A.�Գ���Ϊֱ��x=��1
B.��x����������ͬ�Ľ���
C.���ܹ�ԭ��
D.������4��y1������4��y2���������ߵ����㣬��y1y2��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪ��ABC�����Բ��������̶ȵ�ֱ�ߣ��������������ֱ���ͼ1��ͼ2�л���һ���ң�ʹ�����ҽ���ABC�ֳ������ȵ������֣�������ͼ�ۼ�����д��������
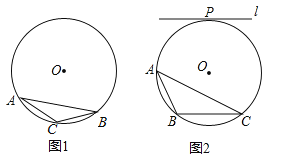
��1����ͼ1��AC=BC��
��2����ͼ2��ֱ��l����O�����ڵ�P����l��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx+c��y��x�IJ��ֶ���ֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��3 | 1 | 3 | 1 |
���н��ۢ������ߵĿ������£�����ͼ��ĶԳ���Ϊx��1���۵�x��1ʱ������ֵy��x����������ܷ���ax2+bx+c��0��һ��������4��������ȷ�Ľ�����_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
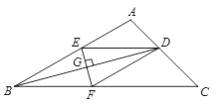
����Ŀ����ͼ���ڡ�ABC�У�BDƽ�֡�ABC��AC��D��EF��ֱƽ��BD���ֱ�AB��BC��BD��E��F��G������DE��DF��
��1����֤��DE=DF��
��2������ABC=30������C=45����DE=4����CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�걱���а��������ղ����ᣬij�̵�Ϊ��ץס��������̻�����������A.B�����������Ʒ��������A�м���Ʒ20����B�ּ���Ʒ10������Ҫ2000Ԫ;������A�м���Ʒ8����B�ּ���Ʒ6������Ҫ1100Ԫ.
(1)��A.B���ּ���Ʒÿ������Ҫ����Ԫ?
(2)�����̵�����ó�10000Ԫȫ���������������ּ���Ʒ�����ǵ��г�����Ҫ��A�ּ���Ʒ������������B�ֵ�6����������B�ּ���Ʒ������8�����蹺��B�ּ���Ʒa��������̵깲�м��ֽ�������?
(3)�ڵ�(2)�ʵ������£�������ÿ��A�ּ���Ʒ�ɻ�����30Ԫ��ÿ��B�ּ���Ʒ�ɻ�����40Ԫ����������ΪyԪ����д��������y(Ԫ)��a(��)�ĺ�����ϵʽ�������ݺ�����ϵʽ˵�����������ʱ�Ľ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ȫУѧ����ѧ�Ľ�ͨ��ʽ����У���꼶��8�����5��ͬѧ���������һ�ݵ����ʾ����Ը�У����ѧ��������������飮��A�������г�����B���˹���������C�����У���D����˽�ҳ�����E��������ʽ������ѡ�Ҫ����ͬѧ���е�ѡ���������������Ƴ�����ͳ��ͼ1������ͳ��ͼ2������������Ϣ������������⣺

��1�����ν��ܵ������������ �ˣ���������ͳ��ͼ����������
��2��������ͳ��ͼ�У�����������������ռ�İٷֱ��� ����������ʽ���������ε�Բ�ĽǶ����� ��
��3����֪��5��ͬѧ����2��Ůͬѧ��Ҫ����ѡ����ͬѧ�㱨���������������б�������״ͼ�ķ��������ǡ��ѡ��1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����70���꣬ijУ���а༶��ӽ�����������У����Ұ��㣬�й��������質����������Һ��ҵ���������ֱ�����ĸA��B��C���α�ʾ����������������ʱ����A��B��C��������ĸ�ֱ�д��3��������Ŀ�Ƭ�����ϣ�ϴ�Ⱥ��������·��������ϣ��ˣ�1�����ȴ��������ȡһ�ſ�Ƭ���Żغ�ϴ�ȣ����ɰˣ�2�������������ȡһ�ſ�Ƭ�����и�ӽ������
��1���ˣ�1������и������Һ��ҵ�������ĸ�����__________��
��2�����û���״ͼ���б��ķ�����ʾ���п��ܵĽ����������ˣ�1����Ͱˣ�2������в�ͬ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�ֱ��MN������A��BE��MN�ڵ�E��CF��MN�ڵ�F��DG��MN�ڵ�G.
(1)��MN�Ƶ�A��ת��ͼ��λ��ʱ����֤:BE +CF =DG; .
(2)��MN�Ƶ�A��ת��ͼ�ں�ͼ��λ��ʱ���߶�BE��CF��DG֮������������������ϵ?
��д����IJ��룬����Ҫ֤��;
(3)��(1)(2)�������£���CD =2AE =6��EF =43����CF= ��
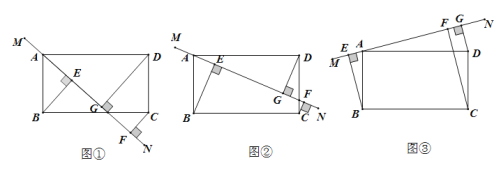
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com