
【题目】已知抛物线y=cx2+2cx-3c(c≠0),则下列说法不正确的是( )
A.对称轴为直线x=-1
B.与x轴有两个不同的交点
C.可能过原点
D.若(-4,y1)、(4,y2)是抛物线的两点,则y1y2>0
【答案】C
【解析】
根据抛物线对称轴公式要求得抛物线的对称轴,由此可判断A;利用Δ的值可判断B;求出x=0时y的值,由此可判断C;分别求出y1、y2的值,由此即可判断D.
抛物线y=cx2+2cx-3c(c≠0),
则抛物线的对称轴为x=-![]() =-1,故A选项正确,不符合题意;
=-1,故A选项正确,不符合题意;
Δ=(2c)2-4c·(-3c)=16c2,
∵c≠0,∴c2>0,
∴Δ>0,
∴抛物线与x轴有两个不同的交点,故B选项正确,不符合题意;
当x=0时,y=-3c≠0,
∴抛物线不经过原点,故C选项错误,符合题意;
当x=-4时,y1=16c-8c-3c=5c,
当x=4时,y2=16c+8c-3c=21c,
∴y1y2=105c2>0,故D选项正确,不符合题意,
故选C.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与双曲线![]() (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是![]() .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线![]() (x>0)的交点有( )
(x>0)的交点有( )

A. 0个B. 1个C. 2个D. 0个,或1个,或2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
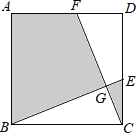
(1)求![]() BGC的度数;
BGC的度数;
(2)若CE=1,H为BF的中点时,求HG的长度;
(3)若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
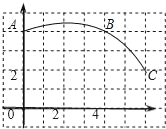
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中CE⊥AB于E,BF⊥AC于F.
(1)求证:△AFB∽△AEC;
(2)求证:△AEFA∽△ABC;
(3)若∠A=60°时,求△AFE与△ABC面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
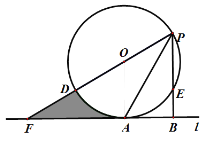
【题目】如图,⊙O的直径PD=8,点E是⊙O上一点,点A是![]() 的中点,连接PA,过点A作直线l⊥PE,垂足为点B,PB=6,直径PD的延长线交直线l于点F.
的中点,连接PA,过点A作直线l⊥PE,垂足为点B,PB=6,直径PD的延长线交直线l于点F.
(1)求证:直线l是⊙O的切线;
(2)求线段PA的长;
(3)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=2x+2m(m>0)与x,y轴分别交于A.B两点,点M是双曲线![]() (x>0)上一点,分别连接MA、MB.
(x>0)上一点,分别连接MA、MB.
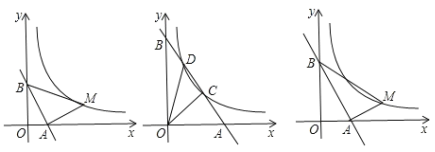
(1)如图,当点A(![]() ,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
(2)如图,当m=3时,直线l与双曲线交于C.D两点,分别连接OC、OD,试求△OCD面积;
(3)如图,在双曲线上是否存在点M,使得以AB为直角边的△MAB与△AOB相似?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com