
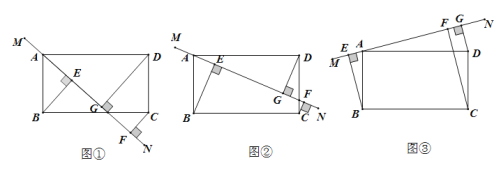
【题目】在矩形ABCD中,直线MN经过点A,BE⊥MN于点E,CF⊥MN于点F,DG⊥MN于点G.
(1)当MN绕点A旋转到图①位置时,求证:BE +CF =DG; .
(2)当MN绕点A旋转到图②和图③位置时,线段BE,CF,DG之间又有怎样的数量关系?
请写出你的猜想,不需要证明;
(3)在(1)(2)的条件下,若CD =2AE =6,EF =43,则CF= 。
【答案】(1)证明见解析;(2)![]() 或
或![]() .
.
【解析】
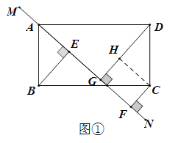
(1)过点C作CH⊥DG于点H,证![]() 和四边形HGFC为矩形即可得出答案;
和四边形HGFC为矩形即可得出答案;
(2)图②过点C作CH⊥BE于点H,可知四边形FCGE为矩形,△BCH≌△DMG即可得出答案,图③过点D作DH⊥CF于点H,可知四边形FCDH为矩形,△ABE≌△DCH,即可得出答案.
解:(1)证明:过点C作CH⊥DG于点H,则∠DHC=∠AEB=90°.
∵∠ABE+∠BAE=90°,∠BAE+∠DAG=90°
∴∠ABE=∠DAG
∵∠DAG+∠ADG=90°,∠ADG+∠CDH=90°,
∴∠DAG=∠CDH
∴∠ABE=∠CDH
在△ABE与△CDH中,∠ABE=∠CDH,∠BEA=∠CHD=90°,AB=DC
∴△ABE≌△CDH
∴BE=DH
![]()
∴四边形HGFC为矩形
![]()
![]()
(2)图②:![]()
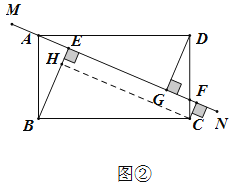
理由:过点C作CH⊥BE于点H,与(1)同理四边形FCGE为矩形,CF=EH,
∴CH∥MN,∠BHC=90°
∴∠HBC+∠HCB=90°
又∵∠HBC+∠ABE=90°
∴∠ABE=∠HCB
∵∠BAE+∠DMG=90°,∠BAE+∠ABE=90°
∴∠DMG=∠ABE=∠HCB
在△BCH与△DMG中,∠BHC=∠DGM=90°,∠HCB=∠DMG,BC=DM
∴△BCH≌△DMG
∴BH=DG
∴![]()
图③:![]()
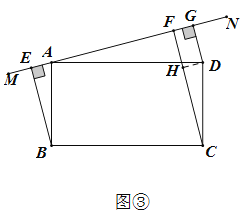
理由:过点D作DH⊥CF于点H,与(1)同理四边形FCDH为矩形,DG=FH,
∵∠CDH+∠ADH=90°,∠ADH+∠GDA=90°
∴∠CDH=∠GDA
∵∠GAD+∠GDA=90°,∠GAD+∠EAB=90°
∴∠GDA=∠EAB
∴∠EAB=∠CDH
在△ABE与△DCH中,∠BEA=∠CHD=90°,∠EAB=∠CDH,AB=DC
∴△ABE≌△DCH
∴BE=CH
∴CF-CH=CF-BE=FH=DG
(3)略


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】直线l:y=2x+2m(m>0)与x,y轴分别交于A.B两点,点M是双曲线![]() (x>0)上一点,分别连接MA、MB.
(x>0)上一点,分别连接MA、MB.
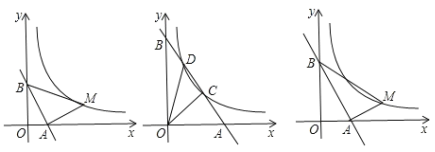
(1)如图,当点A(![]() ,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
,0)时,恰好AB=AM,∠MAB=90°,试求M的坐标;
(2)如图,当m=3时,直线l与双曲线交于C.D两点,分别连接OC、OD,试求△OCD面积;
(3)如图,在双曲线上是否存在点M,使得以AB为直角边的△MAB与△AOB相似?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
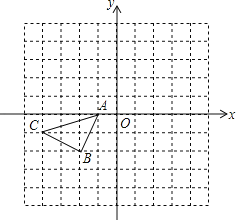
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
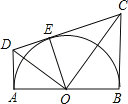
【题目】如图,AB为半圆O的直径,AD、BC分别与⊙O相切于点A,B,CD与⊙O相切于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OE、OC,已知AD=2,BC=4,对于下列结论:①AD+BC=CD:②∠DOC=90°;③S梯形ABCD=![]() CDOA:④OA=2
CDOA:④OA=2![]() .其中结论正确的有_____.(请把正确的结论的序号填在横线上)
.其中结论正确的有_____.(请把正确的结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
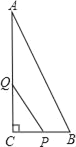
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
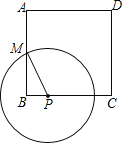
【题目】如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD位于平面直角坐标系中,抛物线y=ax2+bx+c经过菱形的三个顶点A、B、C,已知A(﹣3,0)、B(0,﹣4).
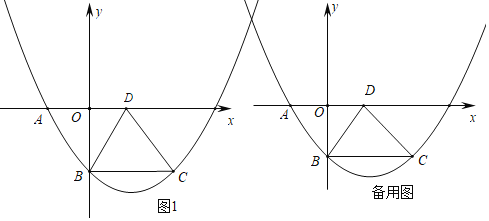
(1)求抛物线解析式;
(2)线段BD上有一动点E,过点E作y轴的平行线,交BC于点F,若S△BOD=4S△EBF,求点E的坐标;
(3)抛物线的对称轴上是否存在点P,使△BPD是以BD为斜边的直角三角形?如果存在,求出点P的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为 (1,n),且与x轴的一个交点在点 (3,0)和 (4,0)之间.则下列结论:①abc>0;②3a+b=0;③a﹣b+c>0;④b2=4a(c﹣n),其中,正确的是_____(填上所有满足题意的序号).
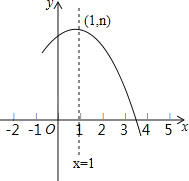
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:

(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com