
【题目】阅读下面材料,并解决问题:

(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
【答案】(1)150°;(2)EF2=BE2+FC2.(3)![]() .
.
【解析】
(1)由△ACP′≌△ABP可得旋转角∠PAP′=60°,可得△APP′为等边三角形,根据勾股定理逆定理可证明△PP′C为直角三角形,根据∠APB=∠AP′C=∠AP′P+∠PP′C即可得答案;(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,由旋转的性质可得AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,根据角的和差关系可得∠EAF=∠E′AF,利用SAS可证明△EAF≌△E′AF,可得E′F=EF,根据等腰直角三角形的性质可得∠E′CF=90°,根据勾股定理即可得结论;(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据含30°角的直角三角形的性质及勾股定理可求出AB、BC的长,根据旋转的性质可得∠A′BC=90°,△BOO′是等边三角形,由∠AOC=∠COB=∠BOA=120°,利用平角的定义可证明C、O、A′、O′四点共线,利用勾股定理求出A′C的长即可得答案.
(1)∵△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PAP′=60°,
∴△APP′为等边三角形,
∴P′P=AP=3,∠AP′P=60°,
∵P′C=PB=4,PC=5,
∴PC2=P′C2+P′P2,
∴△PP′C为直角三角形,且∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°.
故答案为:150°
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠EAE′-∠EAF=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,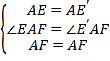
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2.

(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC=![]() ,
,
∵△AOB绕点B顺时针方向旋转60°,∠ABC=30°,
∴∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=![]() ,
,
∴OA+OB+OC=A′O′+OO′+OC=A′C=![]() .
.



科目:初中数学 来源: 题型:
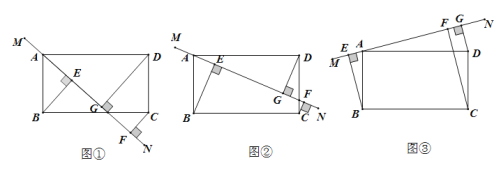
【题目】在矩形ABCD中,直线MN经过点A,BE⊥MN于点E,CF⊥MN于点F,DG⊥MN于点G.
(1)当MN绕点A旋转到图①位置时,求证:BE +CF =DG; .
(2)当MN绕点A旋转到图②和图③位置时,线段BE,CF,DG之间又有怎样的数量关系?
请写出你的猜想,不需要证明;
(3)在(1)(2)的条件下,若CD =2AE =6,EF =43,则CF= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
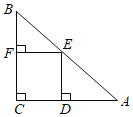
【题目】如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
A. B.
B. C.
C.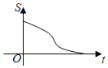 D.
D.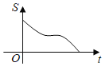
查看答案和解析>>
科目:初中数学 来源: 题型:
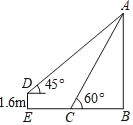
【题目】小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗杆AB的高度.
(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
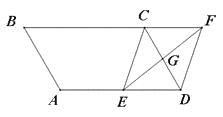
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
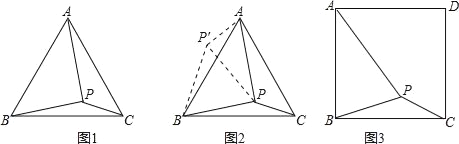
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
小刚同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠APB=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考小刚同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度数的大小和正方形ABCD的边长.
.求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
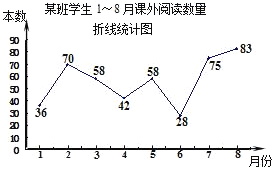
A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
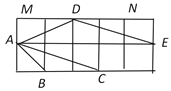
【题目】如图,在2×2的正方形网格中,小正方形的边长均为1,△ABC与△ADE的顶点都在格点上.
(1)求证:△ABC∽△ADE;
(2)求∠MDA+∠NDE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com