
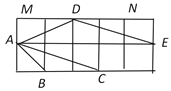
【题目】如图,在2×2的正方形网格中,小正方形的边长均为1,△ABC与△ADE的顶点都在格点上.
(1)求证:△ABC∽△ADE;
(2)求∠MDA+∠NDE的度数.
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:

(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
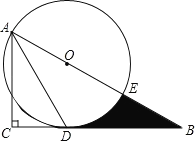
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的顶点坐标为A(1,9),且其图象经过点(﹣1,5)
(1)求此二次函数的解析式;
(2)写出不等式ax2+bx+c>0的解集;
(3)若该函数图象与x轴的交点为B、C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
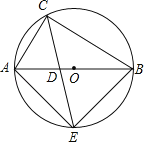
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
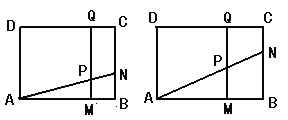
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com