
【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
小刚同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠APB=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考小刚同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度数的大小和正方形ABCD的边长.
.求∠BPC度数的大小和正方形ABCD的边长.
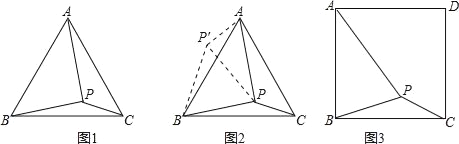
【答案】∠BPC=135°,正方形边长为![]() .
.
【解析】
首先根据旋转的性质得出△BPC≌△BP′A,利用AP′=PC=![]() ,BP=BP′=2得出△AP′P是直角三角形,再利用过点B作BE⊥AP′交AP′的延长线于点E,利用勾股定理得出AB的长.
,BP=BP′=2得出△AP′P是直角三角形,再利用过点B作BE⊥AP′交AP′的延长线于点E,利用勾股定理得出AB的长.
解:如图,将△BPC绕点B逆时针旋转90°,得△BP′A,
则△BPC≌△BP′A.
∴AP′=PC=![]() ,BP=BP′=2.
,BP=BP′=2.
连结P P′,
在Rt△BP′P中,
∵BP=BP′=2,∠PBP′=90°,
∴P P′=2![]() ,∠BP′P=45°.
,∠BP′P=45°.
在△AP′P中,AP′=![]() ,P P′=2
,P P′=2![]() ,AP=
,AP=![]() ,
,
∵(![]() )2+(2
)2+(2![]() )2=(
)2=(![]() )2,即AP′2+PP′2=AP2.
)2,即AP′2+PP′2=AP2.
∴△AP′P是直角三角形,即∠A P′P=90°.
∴∠AP′B=135°.
∴∠BPC=∠AP′B=135°.
如图,过点B作BE⊥AP′交AP′的延长线于点E.
∴∠EP′B=45°.
∴EP′=BE=![]() .
.
∴AE=2![]() .
.
∴在Rt△ABE中,由勾股定理,得AB=![]() .
.
∴∠BPC=135°,正方形边长为![]() .
.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD位于平面直角坐标系中,抛物线y=ax2+bx+c经过菱形的三个顶点A、B、C,已知A(﹣3,0)、B(0,﹣4).
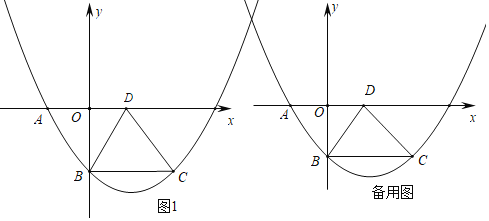
(1)求抛物线解析式;
(2)线段BD上有一动点E,过点E作y轴的平行线,交BC于点F,若S△BOD=4S△EBF,求点E的坐标;
(3)抛物线的对称轴上是否存在点P,使△BPD是以BD为斜边的直角三角形?如果存在,求出点P的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:

(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”又称为端阳节、重午节、龙舟节、正阳节、洛兰节等,是中国四大传统节日之一,端午习俗众多,其中吃粽子是端午节的习俗主题之一,某超市5月以50元/盒的进价购进一款粽子1000盒,以100元/盒的售价全部销售完.销售人员根据市场调研预测,该款粽子每盒的售价在5月售价基础上每降价5元,月销量就会相应增加100盒,该超市6月计划购进该款粽子不超过1400盒.
(1)根据该超市6月计划,该款粽子6月的售价最少每盒可以定价多少元?
(2)实际上,6月该超市购进该款粽子的进价比5月便宜了![]() 元,而实际售价在5月基础上降了m元,已知6月的销售利润比5月增加8%,求m的值.
元,而实际售价在5月基础上降了m元,已知6月的销售利润比5月增加8%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx﹣3与x轴交于A(1,0)、B两点,与y轴交于点C,抛物线的对称轴为直线x=2,交抛物线于点D,交x轴于点E.
(1)请直接写出:抛物线的函数解析式及点B、点D的坐标;
(2)抛物线对称轴上的一动点P从点D出发,以每秒1个单位的速度向上运动,连接OP,BP,设运动时间为t秒(t>0).在点P的运动过程中,请求出:当t为何值时,∠OPB=90°?
(3)如图2,点Q在抛物线上运动(点Q不与点A、B重合),当△QBC的面积与△ABC的面积相等时,请求出点Q的坐标.
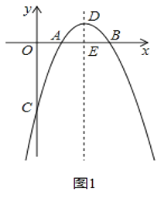
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
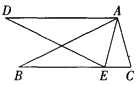
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com