
| A. | x2=2 | B. | x2-(k+1)x+(k+1)=0 | C. | 2x2-$\sqrt{2}$x+1=0 | D. | 1+$\frac{x}{x-1}$=$\frac{1}{x-1}$ |
分析 先计算判别式△=b2-4ac的值,再根据判别式的意义对A、B、C进行判断;通过解分式方程对D进行判断.
解答 解:A、△=0+8=8>0,方程有实数根.故本选项正确;
B、△=[-(k+1)]2-4(k+1)=(k+1)(k-3),当-1<k<3时,△<0,此时方程没有实数根.故本选项错误;
C、△=2-8=-6<0,方程没有实数根.故本选项错误;
D、将原方程去分母,得x-1+x=1,解得x=1,经检验x=1使分母为0,不符合题意;故本选项错误;
故选A.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解分式方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
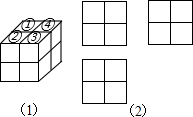 如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.
如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com