
| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
科目:初中数学 来源: 题型:选择题
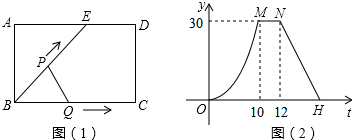
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
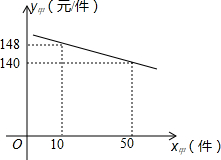 为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示.
为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示. 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | $\sqrt{9}$=±3 | C. | ($\frac{1}{2}$)-1=-2 | D. | (π-3.14)0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
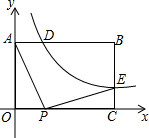 如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一个含有45°角的三角板放在如图所示的两平行线a,b上,测得∠α=125°,则∠β的度数为( )
如图,把一个含有45°角的三角板放在如图所示的两平行线a,b上,测得∠α=125°,则∠β的度数为( )| A. | 60° | B. | 65° | C. | 75° | D. | 80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com