
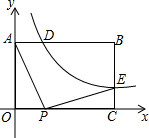
 如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD分析 (1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的长,然后求得点D的坐标,即可求得k的值,继而求得点E的坐标;
(2)首先假设存在要求的点P坐标为(m,0),OP=m,CP=4-m,由∠APE=90°,易证得△AOP∽△PCE,然后由相似三角形的对应边成比例,求得m的值,继而求得此时点P的坐标.
解答 解:(1)∵AB=4,BD=2AD,
∴AB=AD+BD=AD+2AD=3AD=4,
∴AD=$\frac{4}{3}$,
又∵OA=3,
∴D($\frac{4}{3}$,3),
∵点D在双曲线y=$\frac{k}{x}$上,
∴k=$\frac{4}{3}$×3=4;
∵四边形OABC为矩形,
∴AB=OC=4,
∴点E的横坐标为4.
把x=4代入y=$\frac{4}{x}$中,得y=1,
∴E(4,1);
(2)假设存在要求的点P坐标为(m,0),OP=m,CP=4-m.
∵∠APE=90°,
∴∠APO+∠EPC=90°,
又∵∠APO+∠OAP=90°,
∴∠EPC=∠OAP,
又∵∠AOP=∠PCE=90°,
∴△AOP∽△PCE,
∴$\frac{OA}{PC}=\frac{OP}{CE}$,
∴$\frac{3}{4-m}=\frac{m}{1}$,
解得:m=1或m=3,
∴存在要求的点P,坐标为(1,0)或(3,0).
点评 此题属于反比例函数综合题,考查了待定系数求反比例函数解析式、矩形的性质以及相似三角形的判定与性质.注意求得点D的坐标与证得△AOP∽△PCE是解此题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
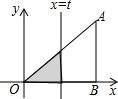 如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )
如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )| A. | 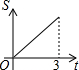 | B. | 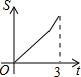 | C. | 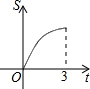 | D. | 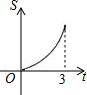 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
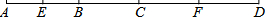 如图,已知B、C是线段AD上任意两点,E是AB的中点,F是CD的中点,若EF=a,AD=b,则线段BC的长是( )
如图,已知B、C是线段AD上任意两点,E是AB的中点,F是CD的中点,若EF=a,AD=b,则线段BC的长是( )| A. | b-a | B. | 2b-a | C. | 2a-b | D. | 2(b-a) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 郑州 | 洛阳 | 开封 | 安阳 | 新乡 | 焦作 | 南阳 | 商丘 |
| 最高气温(℃) | 16 | 11 | 17 | 13 | 11 | 13 | 9 | 11 |
| A. | 11,13 | B. | 11,12.5 | C. | 11,12 | D. | 13,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
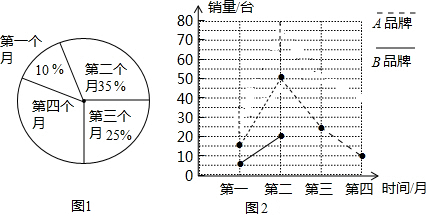
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
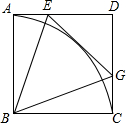 已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作$\widehat{AC}$,连结BG.
已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作$\widehat{AC}$,连结BG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
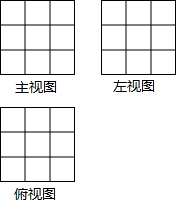 由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )
由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 14个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com