
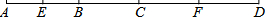 如图,已知B、C是线段AD上任意两点,E是AB的中点,F是CD的中点,若EF=a,AD=b,则线段BC的长是( )
如图,已知B、C是线段AD上任意两点,E是AB的中点,F是CD的中点,若EF=a,AD=b,则线段BC的长是( )| A. | b-a | B. | 2b-a | C. | 2a-b | D. | 2(b-a) |
分析 由已知条件可知,EF=EB+BC+CF=a,得到EB+CF=a-BC,根据E是AB的中点,F是CD中点,AB+CD=2(BE+CF)=2(a-BBC),所以AD=AB+BC+CD=b,即2(a-BC)+BC=b,即可解答.
解答 解:∵EF=EB+BC+CF=a,
∴EB+CF=a-BC,
∵E是AB的中点,F是CD中点
∴AB+CD=2(BE+CF)=2(a-BBC),
∵AD=AB+BC+CD=b,
∴2(a-BC)+BC=b
解得:BC=2a-b.
故选:C.
点评 本题考查了两点间的距离,利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性,同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
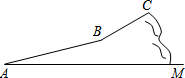 今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.
今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
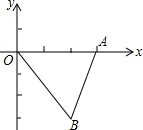 如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )
如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )| A. | ($\frac{5}{3}$,-4) | B. | ($\frac{4}{3}$,-4) | C. | ($\frac{5}{3}$,4) | D. | ($\frac{4}{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
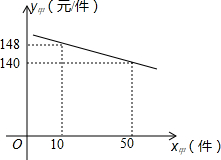 为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示.
为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
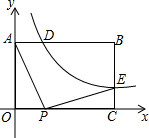 如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
如图,已知矩形OABC中,OA=3,AB=4,双曲线y=$\frac{k}{x}$(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
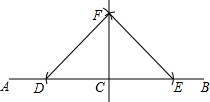 如图,点C在直线AB上,按如下步骤作图:①以点C为圆心,任意长为半径作圆弧,交AB于点D、E;②分别以点D、E为圆心,大于$\frac{1}{2}$DE的长为半径作圆弧,两弧相交于点F;③作直线CF,连结DF、EF.若∠FDC=50°,则∠CFE的大小为40度.
如图,点C在直线AB上,按如下步骤作图:①以点C为圆心,任意长为半径作圆弧,交AB于点D、E;②分别以点D、E为圆心,大于$\frac{1}{2}$DE的长为半径作圆弧,两弧相交于点F;③作直线CF,连结DF、EF.若∠FDC=50°,则∠CFE的大小为40度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com