
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
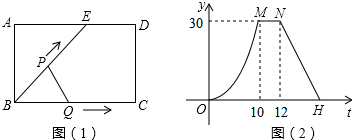
分析 据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解答 解:①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=10cm,S△BCE=$\frac{1}{2}$BC•AB=30,
∴AB=6cm,故①正确;
②根据10-12秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=18,
故点H的坐标为(18,0),
设直线NH的解析式为y=kx+b,
将点H(18,0),点N(12,30)代入可得:$\left\{\begin{array}{l}{18k+b=0}\\{12k+b=30}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=90}\end{array}\right.$.
故直线NH的解析式为:y=-5t+90,故②错误;
③当△ABE与△QBP相似时,点P在DC上,由勾股定理,得AE=8,如图2所示: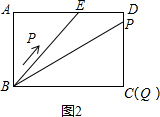
∵tan∠BPQ=tan∠ABE=$\frac{8}{6}$=$\frac{BQ}{PQ}$,
∴$\frac{BQ}{PQ}$=$\frac{4}{3}$,即$\frac{10}{18-t}$=$\frac{4}{3}$,
解得:t=$\frac{11}{5}$,故③正确;
④如图2所示,tan∠PBQ=$\frac{PQ}{BC}$=$\frac{18-t}{10}$=$\frac{\sqrt{3}}{3}$,
解得t=$\frac{54-10\sqrt{3}}{3}$,故④错误;
综上可得①②③正确.
故答案为:①②③.
点评 本题考查了二次函数的综合应用及动点问题的函数图象,根据图(2)判断出点P到达点E时,点Q到达点C是解题的关键,也是本题的突破口,难度较大.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:选择题
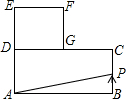 如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )
如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )| A. |  | B. | 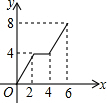 | C. | 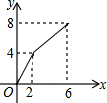 | D. | 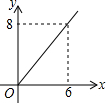 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
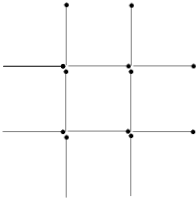 如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.
如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
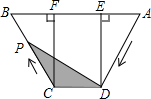 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )| A. | 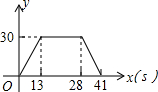 | B. | 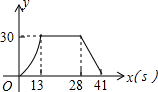 | ||
| C. |  | D. | 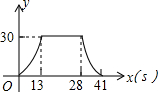 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
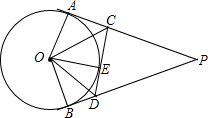 如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
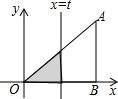 如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )
如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )| A. | 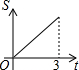 | B. | 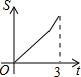 | C. | 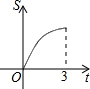 | D. | 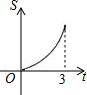 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
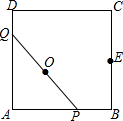 如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.
如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com