
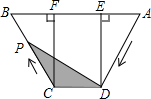
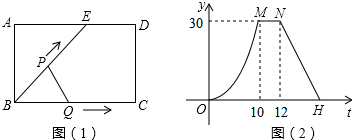
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )| A. | 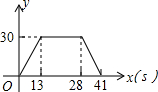 | B. | 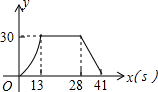 | ||
| C. |  | D. | 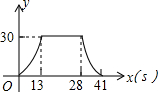 |
分析 分三段考虑,①点P在BC上运动,②点P在BC上运动,③点P在AD上运动,分别求出y与t的函数表达式,继而可得出函数图象.
解答 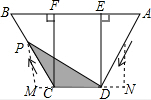 解:在Rt△ADE中AD=$\sqrt{{AE}^{2}{+DE}^{2}}$=13,在Rt△CFB中,BC=$\sqrt{{BF}^{2}{+CF}^{2}}$=13
解:在Rt△ADE中AD=$\sqrt{{AE}^{2}{+DE}^{2}}$=13,在Rt△CFB中,BC=$\sqrt{{BF}^{2}{+CF}^{2}}$=13
①点P在BC上运动:
过点P作PM⊥CD于点M,则PM=CPsin∠B=$\frac{12}{13}$t,
此时y=$\frac{1}{2}$EF×PM=$\frac{30}{13}$t,为一次函数;
②点P在DC上运动,y=$\frac{1}{2}$EF×DE=30;
③点P在AD上运动,过点P作PN⊥CD于点N,则PN=DPsin∠B=$\frac{12}{13}$(AD+CD+BC-t)=$\frac{12(31-t)}{13}$,
则y=$\frac{1}{2}$EF×PN=$\frac{30(31-t)}{13}$=为一次函数.
综上可得选项A的图象符合.
故选A.
点评 本题考查了动点问题的函数图象,解答本题的关键是分段讨论y与t的函数关系式,


科目:初中数学 来源: 题型:解答题
 水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
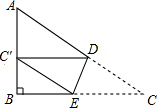 如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
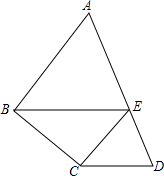 如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.
如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
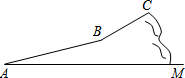 今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.
今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com