
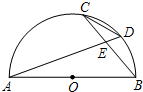
 如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$.
如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$. 分析 连结BD,如图,根据圆周角定理得到∠C=∠A,∠CDE=∠CBA,则可判断△ECD∽△EAB,利用相似比可得$\frac{DE}{BE}$=$\frac{5}{13}$,再由AB是⊙O的直径得到∠ADB=90°,设DE=5x,BE=13x,在Rt△BDE中,根据勾股定理得到BD=12x,然后根据正弦的定义求解.
解答 解:连结BD,如图,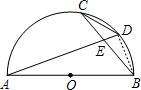
∵∠C=∠A,∠CDA=∠CBA,
∴△ECD∽△EAB,
∴$\frac{DE}{BE}$=$\frac{CD}{AB}$=$\frac{5}{13}$,
∵AB是⊙O的直径,
∴∠ADB=90°,
设DE=5x,BE=13x,
在Rt△BDE中,BD=$\sqrt{B{E}^{2}-D{E}^{2}}$=12x,
∴sin∠BED=$\frac{BD}{BE}$=$\frac{12x}{13x}$=$\frac{12}{13}$.
故答案为$\frac{12}{13}$.
点评 本题考查了相似三角形的判定:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了圆周角定理和解直角三角形.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
 小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)
小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
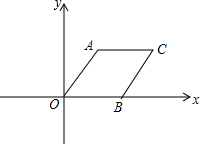 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
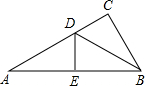 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
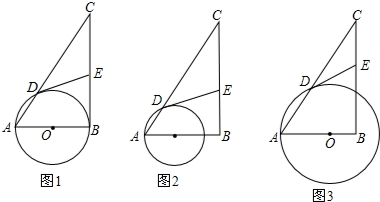
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
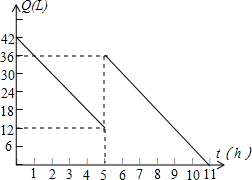 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
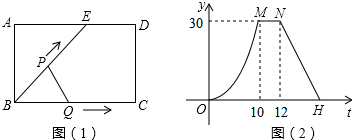
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com