
分析 首先根据根与系数的关系确定方程有两个异号根,然后设α为正β为负,从而将(|α|-β)(|β|-α)≥1化简,然后根据α-β为正,代入求解即可.
解答 解:∵α,β是关于x的方程x2+kx-1=0的两个实根,
∴α+β=-k,αβ=-1,
∴方程必有2个异号根,不妨设α为正β为负,
∵(|α|-β)(|β|-α)≥1,
∴-(α+β)(α-β)≥1 …(1),
又∵α-β为正,
∴(α-β)2=(α+β)2-4αβ=k2+4,
把它们代入(1)式:k$\sqrt{{k}^{2}+4}$≥1…(2)
由 β2-α2≥1>0 及 α为正β为负 知:-β>α>0,所以 α+β=-k<0
即 k>0 …(3)
由(2),(3)解得:k≥$\sqrt{\sqrt{5}-2}$,
故答案为:k≥$\sqrt{\sqrt{5}-2}$.
点评 本题考查了一元二次方程根的分布,确定本题中有两个异号根是解答本题的突破口,能够利用根与系数的关系进行正确的等式变换是解答本题的基础,难度偏大.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:选择题
 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )| A. | 75° | B. | 80° | C. | 85° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
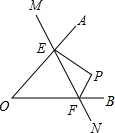 如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com