
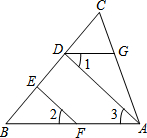
 完成下列证明过程,并在括号中注明理由.
完成下列证明过程,并在括号中注明理由.分析 根据平行线的性质填②、⑤、⑥空,根据平行线的判定填①、③、④空,根据等量代换填⑦.
解答 证明:∵∠ADE+∠CEF=180°(已知)
∴EF∥AD (同旁内角互补两直线平行)
∴∠2=∠3 (两直线平行同位角相等)
∵∠CGD=∠CAB,
∴DG∥AB(同位角相等两直线平行)
∴∠1=∠3 ( 两直线平行内错角相等 )
∴∠1=∠2.(等量代换)
故答案为:已知;同旁内角互补两直线平行;两直线平行同位角相等;DG∥AB(同位角相等两直线平行);∠1=∠3 ( 两直线平行内错角相等 );等量代换.
点评 本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某班对40名学生上学出行方式调查的扇形统计图,问:
如图是某班对40名学生上学出行方式调查的扇形统计图,问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
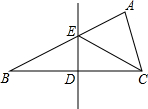 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
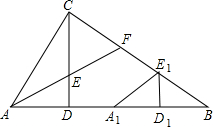 在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.
在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有水分,种子发芽 | B. | 367人中至少有2人的生日相同 | ||
| C. | 三角形的内角和是180° | D. | 小华一出门上学,天就下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com