
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系. 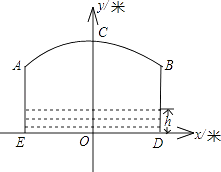
(1)根据题意,填空: ①顶点C的坐标为;
②B点的坐标为;
(2)求抛物线的解析式;
(3)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=﹣ ![]() (t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
【答案】
(1)(0,11);(8,8)
(2)解:∵点C到ED的距离是11米,
∴OC=11,
设抛物线的解析式为y=ax2+11,由题意得B(8,8),
∴64a+11=8,
解得a=﹣ ![]() ,
,
∴y=﹣ ![]() x2+11
x2+11
(3)解:水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为11﹣5=6(米),
∴6=﹣ ![]() (t﹣19)2+8,
(t﹣19)2+8,
∴(t﹣19)2=256,
∴t﹣19=±16,
解得t1=35,t2=3,
∴35﹣3=32(小时).
答:需32小时禁止船只通行
【解析】解:(1)由题意OC=11,OD=8,BD=AE=8, ∴C(0,11),B(8,8),
所以答案是(0,11)和(8,8).


科目:初中数学 来源: 题型:
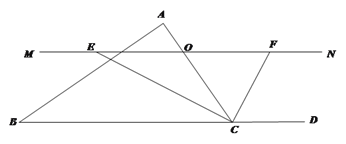
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4![]() )-(-5
)-(-5![]() )+(-4
)+(-4![]() )-3
)-3![]() ;
;
(3)![]() ÷
÷![]() ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. 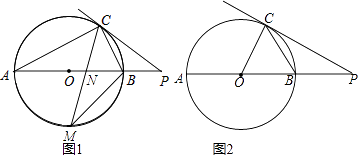
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AEAB;⑤CB∥GD,其中正确的结论是( ) 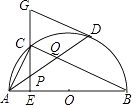
A.①③⑤
B.②④⑤
C.①②⑤
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
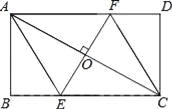
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1. 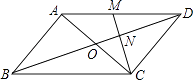
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com