
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AEAB;⑤CB∥GD,其中正确的结论是( ) 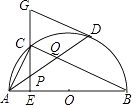
A.①③⑤
B.②④⑤
C.①②⑤
D.①③④
【答案】D
【解析】解:∵在⊙O中,点C是 ![]() 的中点, ∴
的中点, ∴ ![]() =
= ![]() ,
,
∴∠CAD=∠ABC,故①正确;
∵ ![]() ≠
≠ ![]() ,
,
∴ ![]() ≠
≠ ![]() ,
,
∴AD≠BC,故②错误;
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠ACE+∠CAE=∠ABC+∠CAE=90°,
∴∠ACE=∠ABC,
又∵C为 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠CAP=∠ABC,
∴∠ACE=∠CAP,
∴AP=CP,
∵∠ACQ=90°,
∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB
∴根据射影定理,可得AC2=AEAB,故④正确;
如图,连接BD,则∠ADG=∠ABD,
∵ ![]() ≠
≠ ![]() ,
,
∴ ![]() ≠
≠ ![]() ,
,
∴∠ABD≠∠BAC,
∴∠ADG≠∠BAC,
又∵∠BAC=∠BCE=∠PQC,
∴∠ADG≠∠PQC,
∴CB与GD不平行,故⑤错误.
所以答案是:D.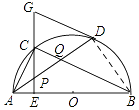
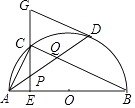
【考点精析】关于本题考查的垂径定理和圆周角定理,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)-5.4+0.2-0.6+1.8
(2) (-26.54)+(-6.4)+18.54+6.4
(3) ![]()
(4)![]()
(5)![]()
(6) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 ![]() 后得到线段CD,则点B的对应点D的坐标为( )
后得到线段CD,则点B的对应点D的坐标为( ) 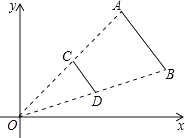
A.(3,3)
B.(1,4)
C.(3,1)
D.(4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系. 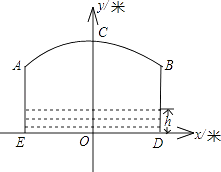
(1)根据题意,填空: ①顶点C的坐标为;
②B点的坐标为;
(2)求抛物线的解析式;
(3)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=﹣ ![]() (t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
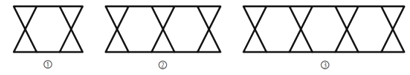
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
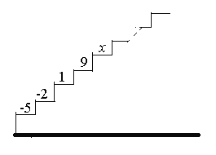
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(3)从下到上前多少个台阶上数的和为30.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E. 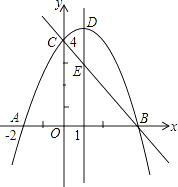
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y= ![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y= ![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ![]() ,则k的值为( )
,则k的值为( )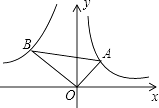
A.﹣3
B.﹣4
C.﹣ ![]()
D.﹣2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com