
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(3)从下到上前多少个台阶上数的和为30.
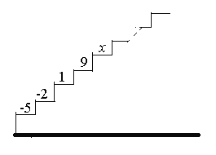
【答案】(1)3;(2)-5;(3)40或51
【解析】
(1)把钱4个台阶上的数字相加即可;(2)根据任意相邻四个台阶上数的和都相等,把第2个台阶至第5个台阶上的数字相加所得的和与(1)中的结果相等,解方程求得x即可;(3)通过(1)(2)的计算,可知台阶上的数字四个一循环,并且4个数字的和为3,①30÷3=10,可知10个循环后所有数字的和为30,此时共有40个台阶;②36+(-5)+(-2)+1=30,36÷3=12,可知第12个循环后所有数字的和加上第13个循环的前3个数的和为30,此时共有12×4+3=51个台阶.由此即可解答.
(1)-5+(-2)+1+9=3.
∴前4个台阶上数的和是3.
(2)由题意得,-2+1+9+x=3,
解得x=-5.
∴第5个台阶上的数x是-5.
(3)通过(1)(2)的计算,可知台阶上的数字四个一循环,并且4个数字的和为3,
①30÷3=10,可知10个循环后所有数字的和为30,此时共有40个台阶;
②36+(-5)+(-2)+1=30,36÷3=12,可知第12个循环后所有数字的和加上第13个循环的前3个数的和为30,此时共有12×4+3=51个台阶.
∴从下到上前40个或51个台阶上数的和为30.


科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. 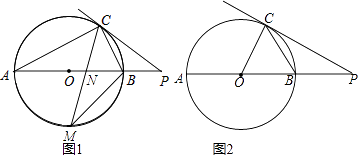
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AEAB;⑤CB∥GD,其中正确的结论是( ) 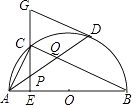
A.①③⑤
B.②④⑤
C.①②⑤
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
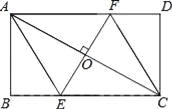
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3,P是AC上一动点,则PB+PE的最小值是( ).

A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1 . 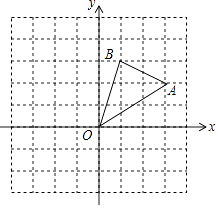
(1)点A关于点O中心对称的点P的坐标为;
(2)在网格内画出△A1OB1;
(3)点A1、B1的坐标分别为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com