
【题目】如图所示,![]() ,
,![]() ,过点D作
,过点D作![]() ,交
,交![]() 的平分线于点E,连接BE,延长DE交BC于F,
的平分线于点E,连接BE,延长DE交BC于F,![]() .
.
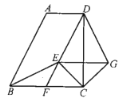
(1)求证:![]() .
.
(2)将![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() 得到
得到![]() ,连接EG.求证:CD垂直平分EG.
,连接EG.求证:CD垂直平分EG.
(3)延长BE交CD于点P,求证:P是CD的中点
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析
【解析】
(1)连接BD,根据平行线的性质以及锐角三角函数的概念找到线段之间的关系,从而证明结论;
(2)根据旋转的性质,只需说明ED=GD,CE=CG,即可证明;
(3)根据已知条件,要证明P是CD的中点,只需证明PD=AD,借助全等即可证明.
(1)如图所示,连接BD.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ∴
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
![]() ,即
,即![]() .
.

(2)∵CE平分![]() ,∴
,∴![]() .
.
由(1)知![]() ,
,
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
由图形旋转的性质知![]() ,
,![]() ,
,
∴![]() ∴C,D都在EG的垂直平分线上,
∴C,D都在EG的垂直平分线上,
∴CD垂直平分EG.
(3)由(2)知![]() ,∴
,∴![]() .
.
∵![]() .∴
.∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
由(1)知![]() .∴
.∴![]() ,
,
∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() .
.
∴P是CD的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
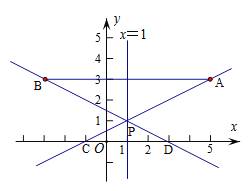
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(-3,3),过点A的直线![]() (m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,已知
,已知![]() .反比例函数
.反比例函数![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,交
,交![]() 于点
于点![]() .
.
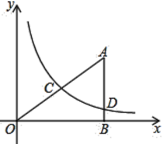
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求经过![]() 、
、![]() 两点的直线所对应的函数表达式;
两点的直线所对应的函数表达式;
(3)设点![]() 是
是![]() 轴上的动点,请直接写出使
轴上的动点,请直接写出使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若直线PE是线段AB的垂直平分线,则![]() ,
,![]() ;②若
;②若![]() ,
,![]() ,则直线PE是线段AB的垂直平分线;③若
,则直线PE是线段AB的垂直平分线;③若![]() ,
,![]() ,则AB垂直平分PE;④若
,则AB垂直平分PE;④若![]() ,则点P必是线段AB的垂直平分线上的点;⑤若
,则点P必是线段AB的垂直平分线上的点;⑤若![]() ,则过点E的直线垂直平分线段AB.其中正确的个数有( ).
,则过点E的直线垂直平分线段AB.其中正确的个数有( ).
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠ADC=22.5°,其中正确的是( )

A. ①③④ B. ③④⑤ C. ①②④ D. ①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 ,中位数在第 组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |

查看答案和解析>>
科目:初中数学 来源: 题型:
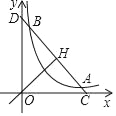
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com