
| 甲 | 10.7 | 10.8 | 10.9 | 10.6 | 11.1 | 10.7 |
| 乙 | 10.9 | 10.9 | 10.8 | 10.8 | 10.5 | 10.9 |
分析 (1)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数;
(2)计算出方差,进一步比较方差的大小得出答案即可.
解答 解:(1)$\overline{x甲}$=$\frac{1}{6}$×(10.7+10.8+10.9+10.6+11.1+10.7)=10.8;
$\overline{x乙}$=$\frac{1}{6}$×(10.9+10.9+10.8+10.8+10.5+10.9)=10.8;
甲的众数是:10.7,乙的众数是:10.9,
甲的中位数是 10.75,乙的中位数是10.85.
(2)S2甲=$\frac{1}{6}$×[(10.8-10.7)2+(10.8-10.8)2+(10.9-10.8)2+(10.6-10.8)2+(11.1-10.8)2+(10.7-10.8)2]≈0.027;
S2乙=$\frac{1}{6}$×[(10.9-10.8)2+(10.9-10.8)2+(10.8-10.8)2+(10.8-10.8)2+(10.5-10.8)2+(10.9-10.8)2]≈0.022;
0.027>0.022
所以乙运动员训练的成绩比较稳定.
点评 本题考查统计知识中的方差、中位数、平均数和众数,掌握计算方法与基本概念是解决问题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
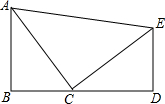 如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )
如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;
(1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com