
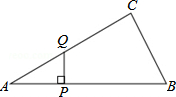
 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )| A. | 2$\sqrt{21}$ | B. | 2$\sqrt{21}$或14 | C. | 2或2$\sqrt{21}$或14 | D. | 2或14 |
分析 分点Q在AC上和BC上两种情况进行讨论表示出三角形的面积,然后根据已知的面积的值得到一元二次方程求解后根据实际意义取值即可.
解答 解:当点Q在AC上时,
∵∠A=30°,AP=x,
∴PQ=xtan30°=$\frac{\sqrt{3}}{3}x$,
∴S=$\frac{1}{2}$×AP×PQ=$\frac{1}{2}$×x×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$x2=14$\sqrt{3}$
解得:x=2$\sqrt{21}$或x=-2$\sqrt{21}$(舍去),
当点Q在BC上时,如下图所示:
∵AP=x,AB=16,∠A=30°,
∴BP=16-x,∠B=60°,
∴PQ=BP•tan60°=$\sqrt{3}$(16-x).
∴S=$\frac{1}{2}$AP×PQ=$\frac{\sqrt{3}}{2}{x}^{2}+8\sqrt{3}$x=14$\sqrt{3}$,
解得:x=2(舍去)或x=14.
故选:B.
点评 本题考查一元二次方程的应用,有一定难度,解题关键是注意点Q在BC上这种情况,同时分类讨论也是中考的热点考点,应加强有关训练.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{34(x+y)}{85(x-y)}$ | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | ||
| C. | $\frac{{y}^{2}{-x}^{2}}{x+y}$ | D. | $\frac{(x+y)^{2}}{{y}^{2}-{x}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小王结婚时,在小区门口的平地上放置了一个充气婚庆拱门,其形状如图所示,若将该拱门(拱门的宽度忽略不计)放在平面直角坐标系中,点A的坐标为(1,0).若将该拱门看作是抛物线y=-$\frac{1}{3}{x}^{2}$+bx-$\frac{7}{3}$的一部分,则点A与点B的距离为( )
小王结婚时,在小区门口的平地上放置了一个充气婚庆拱门,其形状如图所示,若将该拱门(拱门的宽度忽略不计)放在平面直角坐标系中,点A的坐标为(1,0).若将该拱门看作是抛物线y=-$\frac{1}{3}{x}^{2}$+bx-$\frac{7}{3}$的一部分,则点A与点B的距离为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
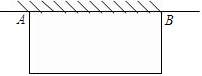 如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?
如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com