【题目】根据下列要求，解答相关问题．

（1）请补全以下求不等式的解集的过程：

① 构造函数，画出图象：根据不等式特征构造二次函数y=；并在下面的坐标系中（图1）画出二次函数y=的图象（只画出大致图象即可）；

② 求得界点，标示所需：当时，求得方程的解为　　　　　　　 ；并用虚线标示出函数y=图象中＜0的部分；

③借助图象，写出解集：由所标示图象，可得不等式＜0的解集为 ．

（2）请你利用上面求不等式解集的过程，求不等式-3≥0的解集．

参考答案：

【答案】（1）①见解析；② ;③ ;(2) x≥3或x≤-1

【解析】试题分析：（1）画出二次函数y=x2-2x的图象，利用图象法求出方程x2-2x=0，以及不等式x2-2x＜0的解即可．

（2）画出函数y=x2-2x-3的图象，利用图象法即可解决问题．

试题解析：（1）二次函数y=x2-2x的图象如图1所示，

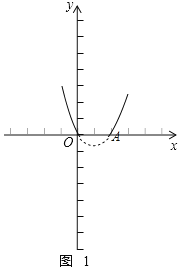
∵二次函数y=x2-2x与x轴交于O（0，0），A（2，0），

∴方程x2-2x=0的解为x=0或2．

由图象可知x2-2x＜0的解集为0＜x＜2．

故答案为x=0或2，0＜x＜2．

（2）函数y=x2-2x-3的图象如图2所示，

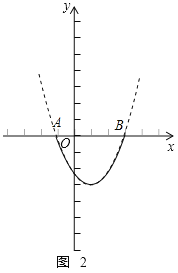
∵A（-1，0），B（3，0），

∴不等式x2-2x-3≥0的解集，由图象可知，x≥3或x≤-1．

关闭