
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?

【答案】(1)5厘米;(2)当t为 ![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
【解析】
(1)作DE⊥BC于E,则四边形ADEB是矩形,在直角△DEC中运用勾股定理即可求解;
(2)由题意可知BP=t厘米,则PC=(5﹣t)厘米,CQ=2t厘米,同时由题意可知0<t≤2.5;作QH⊥BC于点H,运用三角形相似可求解QH的长度表达式,则可列出△DEC的面积表达式,再按线段PQ将四边形ABCD的面积分为1:2两部分,分S△PQC:S四边形ABCD=1:3和S△PQC:S四边形ABCD=2:3两种情况分别讨论.
(1)解:如图1,作DE⊥BC于E,则四边形ADEB是矩形.
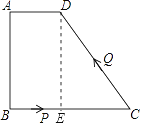
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2 ,
∴DC= ![]() =5厘米;
=5厘米;
(2)解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
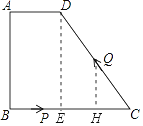
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴QH= ![]() t,
t,
∴S△PQC= ![]() PCQH=
PCQH= ![]() (5﹣t)
(5﹣t) ![]() t=﹣
t=﹣ ![]() t2+3t,
t2+3t,
S四边形ABCD= ![]() (AD+BC)AB=
(AD+BC)AB= ![]() (1+5)×3=9,
(1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+5=0,
×9,即t2﹣5t+5=0,
解得t1= ![]() ,t2=
,t2=![]() (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+10=0,
×9,即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为 ![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
秒时,线段PQ将四边形ABCD的面积分为1:2两部分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程![]() (
(![]() )与行驶的时间
)与行驶的时间![]() (
(![]() )之间的函数关系,如图中线段
)之间的函数关系,如图中线段![]() 所示,慢车离乙地的路程
所示,慢车离乙地的路程![]() (
(![]() )与行驶的时间
)与行驶的时间![]() (
(![]() )之间的函数关系,如图中线段
)之间的函数关系,如图中线段![]() 所示,则快、慢车相距225
所示,则快、慢车相距225![]() 时,行驶的时间是( )
时,行驶的时间是( )

A.1![]() B.3
B.3![]() C.1
C.1![]() 或3
或3![]() D.2
D.2![]() 或4
或4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
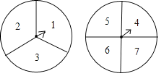
【题目】两个自由转动的转盘如图所示,一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,另一个分为
,另一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() .转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面
.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面![]() ,
,![]() 两种方案中选一种:方案
两种方案中选一种:方案![]() :猜“奇数”或猜“偶数”其中的一种;方案
:猜“奇数”或猜“偶数”其中的一种;方案![]() :猜“是
:猜“是![]() 的整数倍”或猜“不是
的整数倍”或猜“不是![]() 的整数倍”其中的一种.
的整数倍”其中的一种.
![]() 如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
![]() 为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于C,D,交AB于E,AF为⊙O的直径,下列结论中正确的有:①∠ABP=∠AOP;②AP=BP;③弧BC=弧DF ;④∠APO=∠BPO;⑤AB⊥PD.
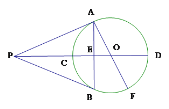
A. ①⑤ B. ②③⑤ C. ①④ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
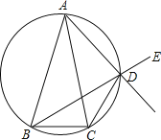
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角尺ABC和ADE如图摆放,∠CAB=∠DAE=90°,∠ACB=∠DEA=30°,使点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ACE为等边三角形.其中正确的是( )
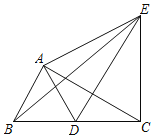
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com