
【题目】如图,在平面直角坐标系中,A,B两点分别在x轴和y轴上,OA=1,OB= ![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 . 
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,M是平行四边形ABCD的AB边中点,CM交BD于点E,则图中阴影部分的面积与平行四边形ABCD的面积的比是( )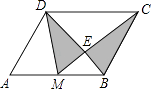
A.1:3
B.1:4
C.1:6
D.5:12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥HD,EG平分∠AEC,EG∥AB,AF平分∠BAE,CE的延长线交AF于点F,若∠HCE=![]() °,∠F=
°,∠F=![]() °,用含
°,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() =_______
=_______
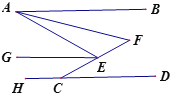
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为1,宽为![]() 的长方形纸片
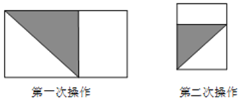
的长方形纸片![]() 如图那样折一下,剪下一个边长等于长方形的宽度的正方形
如图那样折一下,剪下一个边长等于长方形的宽度的正方形![]() 称为第一次操作
称为第一次操作![]() ;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形
;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形![]() 称为第二次操作
称为第二次操作![]() ;如些反复操作下去,若在第
;如些反复操作下去,若在第![]() 次操作后剩下的长方形为正方形,则操作终止.
次操作后剩下的长方形为正方形,则操作终止.
![]() 第一次操作后,剩下的长方形两边长分别为______和 ;
第一次操作后,剩下的长方形两边长分别为______和 ;![]() 用含
用含![]() 的代数式表示
的代数式表示![]()
![]() 若第二次操作后,剩下的长方形恰好是正方形,则求
若第二次操作后,剩下的长方形恰好是正方形,则求![]() 的值,写出解答过程;
的值,写出解答过程;
![]() 若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求
若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
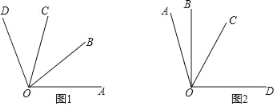
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com